Differential Evolution veranschaulicht
Dieser Beitrag bezieht sich auf PGAPack und PGApy oder andere Genetische Algorithmus (GA) Implementierungen die Differential Evolution (vielleicht übersetzbar mit Differentielle Evolution, in der Folge abgekürzt mit DE) unterstützen.
Differential Evolution (DE) [1], [2], [3] ist ein Optimierungsalgorithmus der ähnlich wie andere evolutionäre Algorithmen auf einer Population basiert. Der Algorithmus ist recht mächtig, in PGAPack implementiert und auch in PGAPy nutzbar. Um einige Punkte zu diesem Algorithmus zu veranschaulichen habe ich einen einfachen Parcours in OpenSCAD konstruiert.
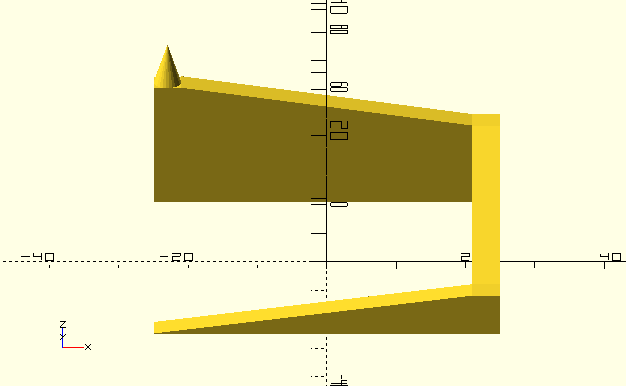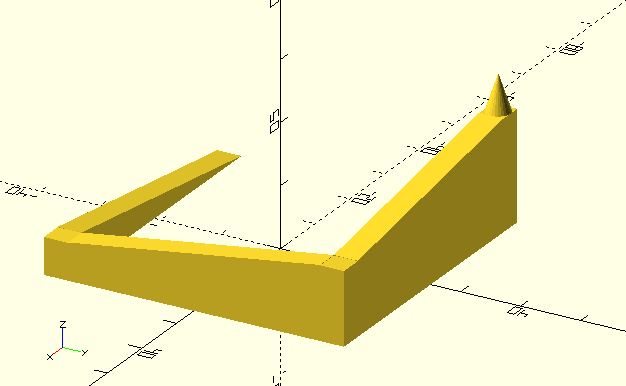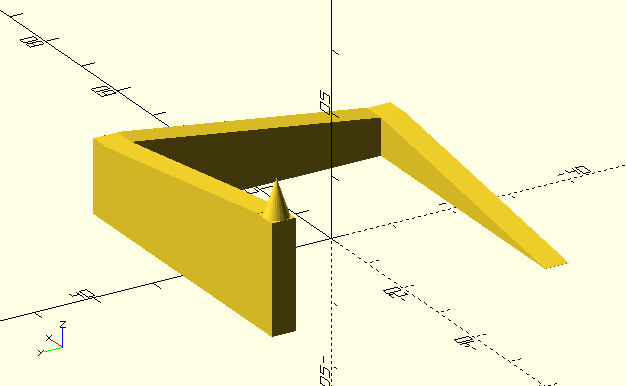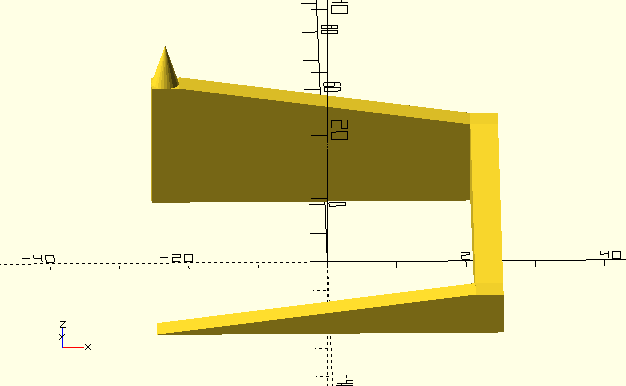
Um den Optimierer mit diesem Parcours zu testen ist das Gen (DE nennt es die Parameter) die X- und Y-Koordinate um eine Position im Parcours zu bestimmen. In der Folge bezeichnen wir diese zwei Werte auch als Vektor, wie das in der Literatur zu DE üblich ist. Wir initialisieren die Population in der Gegend beim Start der Rampe. Wir erlauben der Population, den Initialisierungsbereich zu verlassen.
Es ist zu beachten, dass die Ecken des Parcours flach sind, dass dort also alle Punkte die selbe Höhe haben. Solche Bereiche sind generell schwierig für Optimierungsalgorithmen weil der Algorithmus nicht wissen kann, in welche Richtung bessere Werte (wenn es diese überhaupt gibt) zu finden sind. Dies ist auch der Grund, warum wir den Initialisierungsbereich nicht in den flachen Bereich am Boden des Parcours legen. Üblicherweise würde man nämlich die Population über den gesamten zu durchsuchenden Bereich initialisieren. In diesem Fall möchten wir demonstrieren, dass der Algorithmus auch fähig ist, eine Lösung weit vom Initialisierungsbereich zu finden.
Der DE Algorithmus ist recht einfach (siehe z.B. [3] S.37-47): Mit jedem Vektor \(\mathbf x_{i,g}\) der Population der aktuellen Generation \(g\), wobei \(i\) der Populationsindex ist wird ein Genaustausch mit einem Mutanten-Vektor vorgenommen. Der Mutanten-Vektor wird zufällig (ohne Zurücklegen) aus drei Populations-Vektoren bestimmt, indem diese wie folgt kombiniert werden.
Wie man sieht, wird eine gewichtete Differenz von zwei Vektoren der
Population gebildet und zu einem dritten Vektor addiert. Alle Indices
\(r_0, r_1,\) und \(r_2\) sind voneinander und von \(i\)
verschieden. Das Gewicht \(F\) ist ein Konfigurationsparameter der
typischerweise \(0.3 \le F < 1\) ist. Der beschriebene Algorithmus
ist der klassische DE Algorithmus, oft auch als de-rand-1-bin
bezeichnet. Eine Variante nutzt statt einem zufälligen Index \(r_0\)
den Index des besten Vektors und wird als de-best-1-bin bezeichnet.
Falls mehr als zwei Differenzen addiert werden wäre eine andere Variante
z.B. de-rand-2-bin. Die letzte Komponente der Bezeichnung steht für
Uniform Crossover [4], eine binomiale Verteilung. In DE werden die
Parameter des Mutanten-Vektors mit einer bestimmten Wahrscheinlichkeit
\(Cr\) ausgewählt. Man beachte, dass DE dafür sorgt, dass zumindest
ein Parameter des Mutanten-Vektors ausgewählt wird (sonst bliebe der
betrachtete Original-Vektor \(\mathbf x_{i,g}\) unverändert).
Mehr Details zu DE und er Nutzung mit PGAPack findet sich in den Abschnitten Differential Evolution und Mutation der PGAPack Dokumentation.
Um das OpenSCAD Modell in der Optimierung zu verwenden, wird es mithilfe eines STL zu PNG Konverters in ein Graustufen-Höhenbild umgewandelt (STL ist ein 3D-Format das von OpenSCAD generiert werden kann). Die Bewertungsfunktion des Algorithmus liefert dann einfach den Graustufen-Wert an der gegebenen X/Y-Position zurück (nach Rundung der Gen-Werte und Konvertierung in einen Integer-Wert). Werte ausserhalb des Bildes werden als 0 (schwarz) geliefert. Der resultierende Optimierungslauf ist unten in einem animierten Bild dargestellt. Die Population ist ziemlich klein und enthält nur 6 Vektoren. Wir sehen dass, wenn die Abstände zwischen den Punkten groß werden (auf den geraden Strecken des Parcours), die Optimierung in größeren Schritten voranschreitet. Wir sehen auch, dass der Algorithmus in den flachen Ecken einige Zeit brauchen kann bis er aus diesem Bereich entkommt. Schließlich, in der letzten Ecke, wird der Kegel erklommen und der Algorithmus stoppt wenn das erste Individuum eine Bewertung mit dem größten Graustufen-Wert liefert (entspricht weiss). Bitte beachten, dass ich ein bisschen geschummelt habe: Viele Optimierungläufe dauern deutlich länger (Insbesondere in den flachen Bereichen kann der Algorithmus längere Zeit stecken bleiben). Ich habe einen Lauf ausgewählt der sich für eine Animation gut eignet. Dieser Lauf ist nicht im Bereich des Durchschnitts sondern deutlich kürzer.
