Seit einiger Zeit optimiere ich Antennen mit Genetischen Algorithmen. Ich verwende dafür das Paket für parallele Genetische Algorithmen, pgapack das ursprünglich von David Levine vom Argonne National Laboratory entwickelt wurde und das ich pflege (wie übersetze ich "maintain"?). Noch länger als die Pflege von pgapack entwickle ich eine Python Bibliothek für pgapack namens pgapy.

Für die Antennensimulation verwende ich Tim Molteno's PyNEC Paket, eine Bibliothek in Python für ein Paket zur elektromagnetischen Simulation namens "Numerical Electromagnetics Code (NEC) Version 2", geschrieben in C++ (auch bekannt als NEC++).

Mit diesen Paketen habe ich ein kleines Open Source Framework für die Antennen-Optimierung namens antenna-optimizer geschrieben. Dieses kann traditionelle Genetische Algorithmen mit Bit-Strings als Genen als auch Fließkomma-Repräsentationen mit dafür geeigneten Operatoren verwenden.

Das "Parallel" in pgapack sagt uns, dass die Evaluierungsfunktion des Genetischen Algorithmus parallelisiert werden kann. Bei der Optimierung von Antennen simulieren wir für jede Paramter-Kombination die einen Antenne darstellt diese mit PyNEC. Antennensimulation ist nach wie vor (der ursprüngliche NEC Code ist aus den 80er Jahren und wurde im Zeitalter von Lochkarten entwickelt) ein CPU-instensives Unterfangen. So ist es eine gute Nachricht, dass wir mit pgapack viele Simulationen parallel mit dem Message Passing Interface (MPI) Standard [1] durchführen können.

Für pgapack – und damit auch für pgapy – habe ich in letzter Zeit einige bewährte klassische Algorithmen implementiert:

• Differential Evolution [2], [3], [4] ist ein erfolgreicher Optimierungs-Algorithmus für Fließkomma-Gene der für elektromagnetische Aufgaben sehr interessant ist.

• Der "elitist Nondominated Sorting Genetic Algorithm" NSGA-II [5] erlaubt es in einem einzigen Optimierungslauf mehrere Zielfunktionen zu optimieren

• Wir können Wertebeschränkungen im Zielbereich einer Funktion definieren die minimiert werden, sogenannte "Constraints" [6]. Damit eine Lösung gültig ist, müssen alle Constraints 0 oder negativ sein.

Traditionell ist mit Genetischen Algorithmen nur eine Evaluierungsfunktion, die sogenannte Zielfunktion möglich. Mit NSGA-II können mehrere Zielfunktionen oder Kriterien verwendet werden. Das Englische nennt solche Algorithmen "Multi-Objective Optimization" (Optimierung mehrerer Ziele).

Für die Antennensimulation heisst dass, wir müssen nicht mehrere Kriterien für eine gute Antenne wie Gewinn, Vorwärts/Rückwärtsverhältnis und Stehwellenverhältnis (SWV) in einer einzigen Evaluierungsfunktion zusammenfassen, was ich bisher im antenna-optimizer gemacht habe, sondern können sie separat definieren und dem Genetischen Algorithmus die Optimierung überlassen.

Mit mehreren Zielfunktionen ist es allerdings typischerweise so, dass die Verbesserung bei einem Ziel eine Verschlechterung bei einem anderen Ziel zur Folge hat und umgekehrt. Wir suchen also Lösungen die strikt besser sind als andere Lösungen. Eine Lösung dominiert eine andere Lösung wenn sie in einem Kriterium besser aber in keinem der anderen Kriterien schlechter ist als die andere Lösung. Alle Lösungen die dieser Definition entsprechen heissen Pareto-Optimal nach dem Italienischen Wissenschaftler Vilfredo Pareto der das Konzept von Pareto-Optimalität zuerst definiert hat. Alle Lösungen die dieses Optimalitäts-Kriterium erfüllen, liegen auf einer sogenannten Pareto-Front. Wenn wir nur zwei Zielfunktionen haben, können wir die Pareto-Front gut mit einem Scatterplot (Streudiagramm) darstellen, wie wir weiter unten sehen werden.

Weil pgapack einen Ansatz verfolgt, der die freie Kombination von Algorithmen unterstützt, können wir verschiedene erfolgreiche Strategien für unterschiedliche Teile des Genetischen Algorithmus kombinieren:

• Für den Mutation/Crossover Teil können wir Differential Evolution (DE) verwenden

• DE wiederum kann für mehrere Zielfunktionen mit der (Generations-) Ersetzungsstrategie von NSGA-II kombiniert werden

• Wir können einige der Zielfunktionen als Beschränkungen (Constraints) definieren. Für unser Problem ist es sinnvoll nur Antennen zu erlauben die ein bestimmtes Stehwellenverhältnis (SWV) nicht überschreiten. Wir erlauben also keine Antenne mit einem SWV > 1.8. Die zugehörige Zielfunktion ist \(S - 1.8 \le 0\) wobei \(S\) das SWV ist.

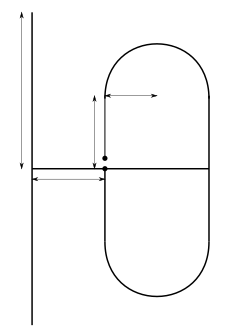
Mit dieser Kombination können wir erfolgreich Antennen für das 70cm Amaterufunkband (430 MHz - 440 MHz) berechnen. Die Antenne verwendet einen sogenannten Faltdipol (das Ding mit den Rundungen in der Grafik) und ein gerades Element. Die Messlinien in der Grafik repräsentieren die vom Genetischen Algorithmus optimierten Längen. Die zwei Punkte in der Mitte des Faltdipols zeigen den Punkt wo die Speiseleitung angeschlossen wird.

Ein erstes Beispiel simuliert Antennenparameter für die höchste, niedrigste und mittlere Frequenz. Der Gewinn und das Vorwärts/Rückwärtsverhältnis (Forward/Backward ratio in der Grafik) werden nur für die mittlere Frequenz berechnet:

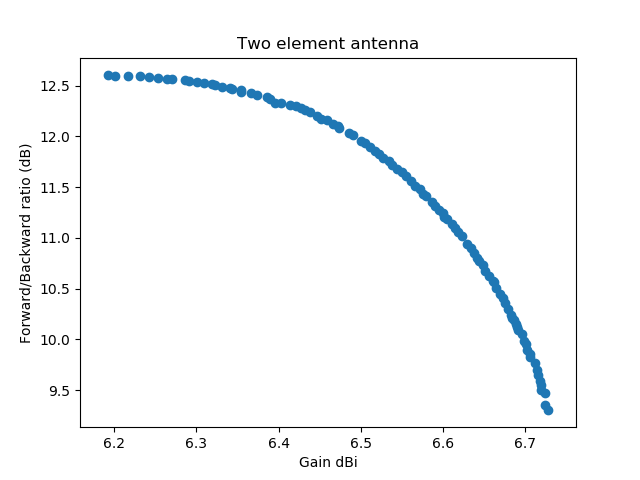
In dieser Grafik (ein Scatterplot) wird die erste Zielfunktion (der Gewinn) gegen die zweite Zielfunktion, das Vorwärts/Rückwärtsverhältnis aufgetragen. Alle Zahlen sind für die mittlere Frequenz. Jeder Punkt in der Grafik repräsentiert eine Antenne. Alle Antennen haben ein SWV kleiner als 1.8 auf der kleinsten, mittleren und höchsten Frequenz.

Nach diesem Erfolg habe ich dann angefangen, mit unterschiedlichen Einstellungen für die Parameter des Differential Evolution (DE) Algorithmus zu experimentieren. Es ist in der Literatur zu DE bekannt dass für "zerlegbare" (decomposable) Probleme eine niedrige Crossover-Rate besser ist, für nicht-zerlegbare eine höhere. Ein zerlegbares Problem zeichnet sich dadurch aus, dass die unterschiedlichen Dimensionen getrennt voneinander optimierbar sind, dies wurde zuerst von Salomon 1996 [7] beobachtet. Ursprünglich hatte ich eine Crossover-Rate von 0.2 eingestellt und meine Hoffnung war, dass die Optimierung mit einer höheren Rate besser und schneller funktionieren würde. Das Experiment unten verwendet eine Crossover-Rate von 0.9.

Zusätzlich habe ich mit "Dither" für den Skalierungsfaktor \(F\) von Differential Evolution (könnte vielleicht mit einem leichten "Zittern" Skalierung übersetzen) experimentiert. Mit diesem Faktor wird die Differenz von zwei Vektoren der Input-Parameter bei der Anwendung von DE multipliziert. In der ersten Implementierung hatte ich Dither auf 0 gesetzt, jetzt hatte ich 0.2 eingestellt. Ich war dann sehr überrascht dass ich mit diesen Einstellungen eine neue Pareto-Front als Lösung gefunden habe:

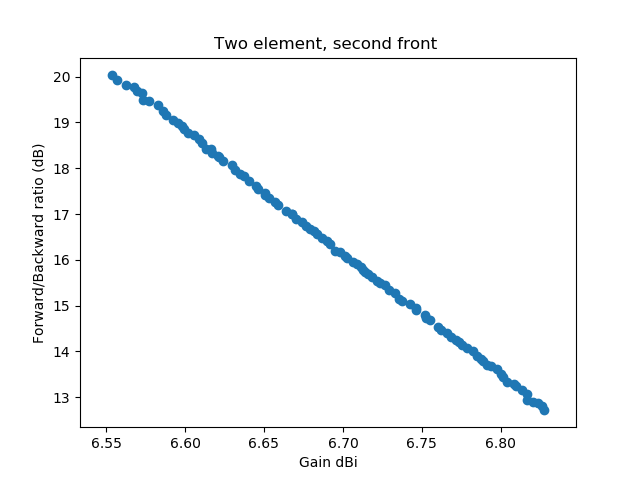
Damit man besser sieht, dass die zweite Front komplett die zuerst gefundene Front dominiert habe ich beide in einer Grafik geplottet:

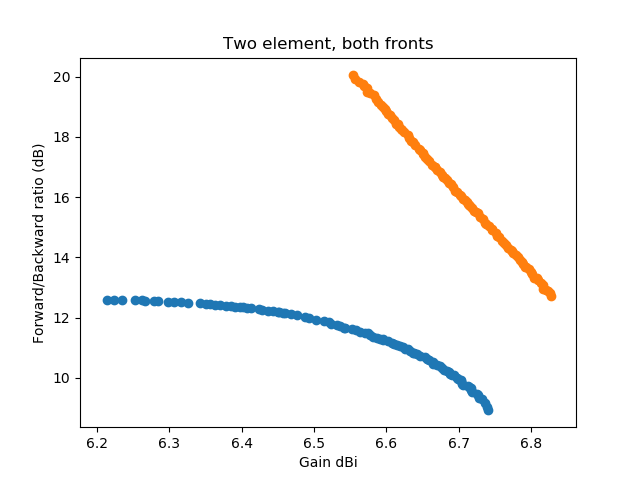
Weil diese zweite Front (über den gesamten Frequenzbereich) für eine Zwei-Elemente Antenne zu gut ausschaut um wahr zu sein schauen wir uns das im Folgenden genauer an. Zuerst schauen wir auf die Orientierung der Antenne und des berechneten Gewinn-Diagramms für eine der Antennen in der Mitte der unteren Front:

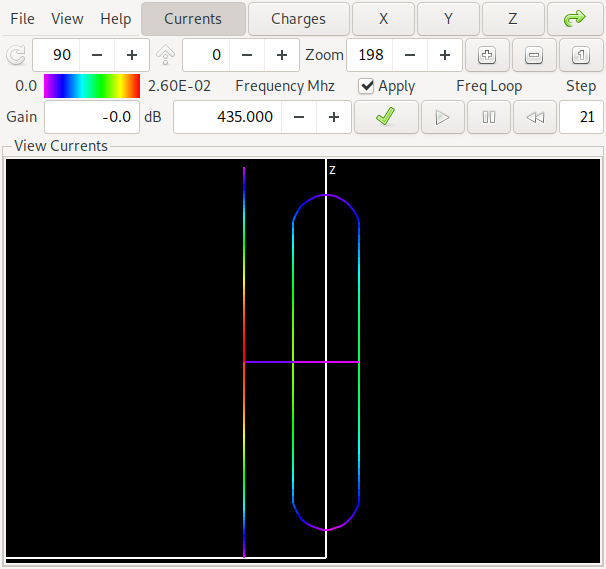
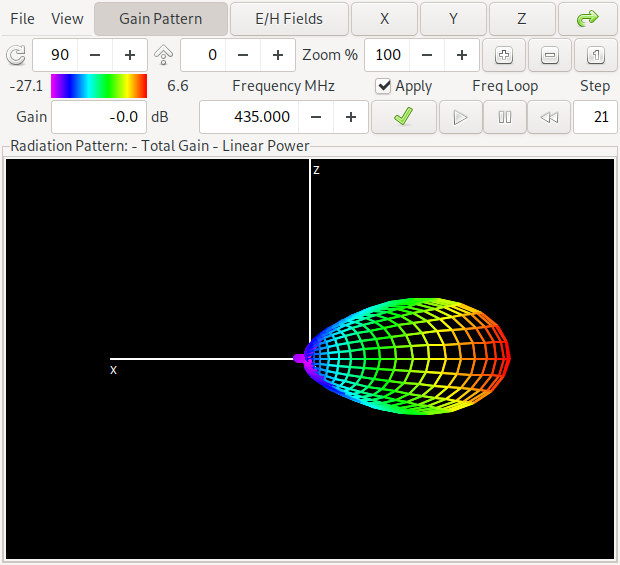
Die Antenne hat – wie schon aus der ersten Pareto-Front Grafik zu entnehmen – einen Gewinn von etwa 6.6 dBi und ein Vorwärts/Rückwärtsverhältnis von etwa 11 dB in der Mitte des Bandes bei 435 MHz. Die Einfärbung der Antenne deutet die Ströme in der Antennenstruktur an. Wer sich das selbst anschauen möchte: Hier ist ein Link zur NEC Input Datei für Antenne 1.

Vergleichen wir diese Antenne mit einer aus der Mitte der "orangen Front" wo wir deutlich bessere Ergebnisse bekommen:

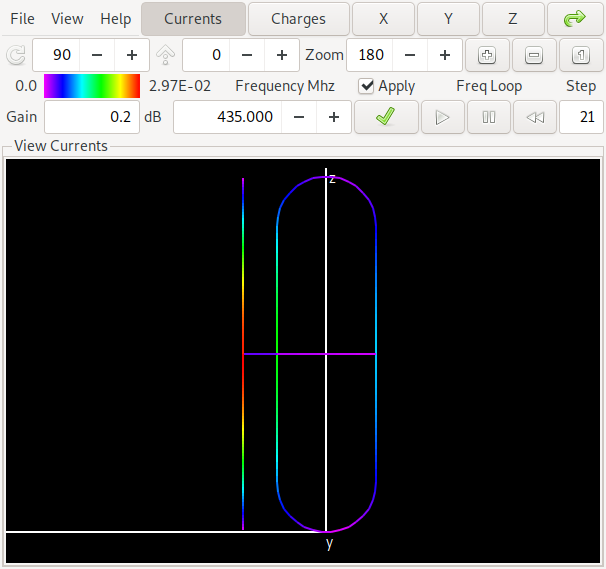
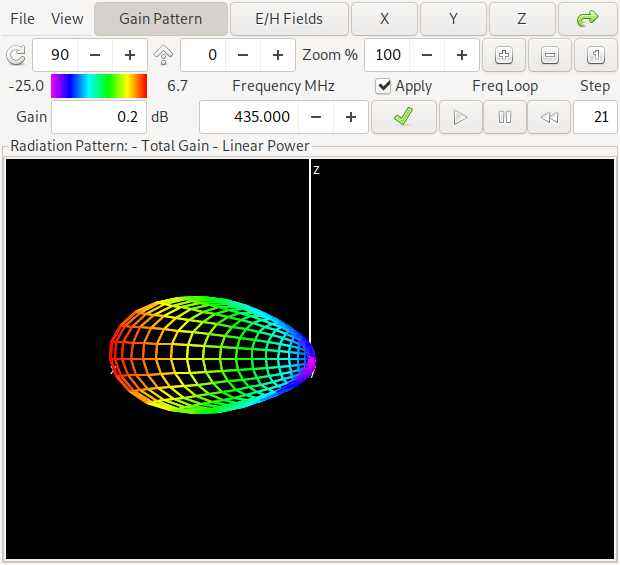
Diese Antenne ist aus der Mitte der oberen Pareto-Front und hat einen Gewinn von etwa 6.7 dBi sowie ein Vorwärts/Rückwärtsverhältnis von etwa 16 dB in der Mitte des Bandes bei 435 MHz. Wer entdeckt den Unterschied zur vorherigen Antenne? Ja: der maximale Gewinn liegt in der Gegenrichtung der ersten Antenne. Wir sagen dass bei der ersten Antenne das gerade Element ein Reflektor ist, während bei der zweiten Antenne das gerade Element als Direktor arbeitet. Auch hier ist ein Link zur NEC Input Datei für Antenne 2.

Nun schauen wir uns über die ganze Frequenz den Gewinn und das Vorwärts/Rückwärtsverhältnis an. Die linke Grafik ist für die erste Antenne (die mit dem Reflektor-Element), die rechte für die zweite Antenne wo das gerade Element als Direktor arbeitet.

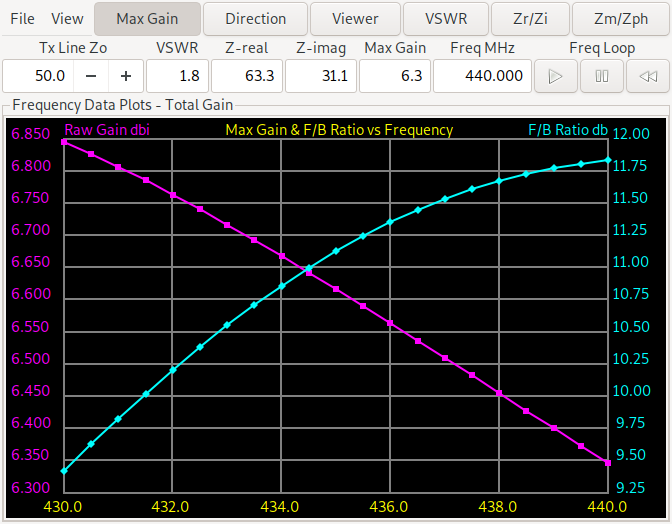
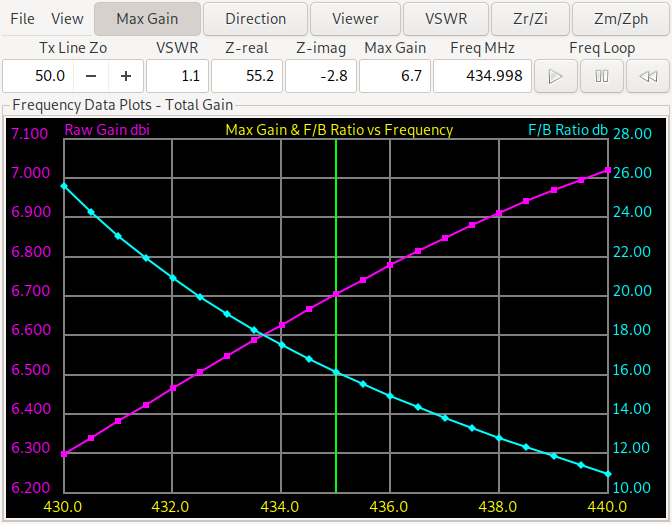
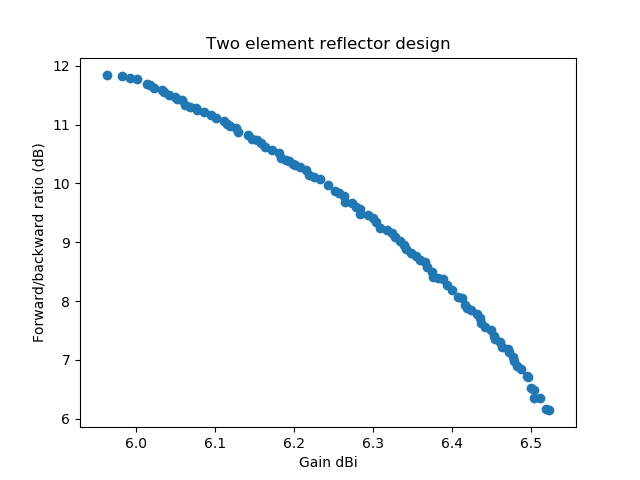
Wir sehen dass sich das Vorwärts/Rückwärtsverhältnis bei der Direktor Antenne von etwas mehr als 10 dB bis zu über 25 dB bewegt, während es für das Reflektor-Design von 9.3 dB bis 11.75 dB geht. Der Minimalgewinn ist beim Reflektor-Design etwas besser (6.35-6.85 dBi bzw. 6.3-7.05 dBi). Also brauchen wir weitere Experimente. Wenn man die Lösungen auf ein Reflektor-Design beschränkt und fordert dass der Minimalgewinn und das minimale Vorwärts/Rückwärtsverhältnis an den drei Stellen (untere, mittlere, obere Frequenz) genommen wird bekommen wir:

Für das gleiche bei einem Direktor Design (auch mit minimalem Gewinn und Vorwärts/Rückwärtsverhältnis bei allen drei Frequenzen (untere, mittlere, obere Frequenz) bekommen wir:

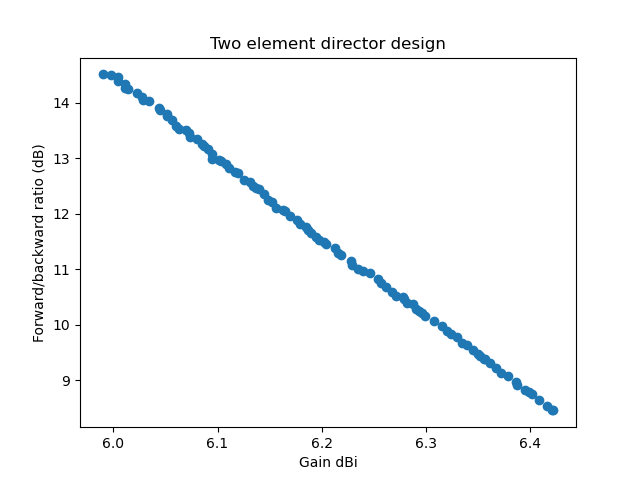
Mit diesen Resultaten ist der Sweet Spot für eine Antenne die man wirklich bauen will wahrscheinlich bei etwa 10 dB Vorwärts/Rückwärtsverhältnis oder darüber und bei einem Gewinn von etwa 6.2 dBi. Ein paar zehntel-dB mehr Gewinn rauszuholen und dabei mehrere dB Vorwärts/Rückwärtsverhältnis zu verlieren scheint nicht sehr sinnvoll. Beim Vergleich des Direktor mit dem Reflektor-Design fällt auf (was zumindest meiner Intuition widerspricht) dass das Direktor-Design ein besseres Vorwärts/Rückwärtsverhältnis über den gesamten Frequenzbereich hat. Wenn allerdings die Antenne für Relais-Kommunikation Verwendung finden soll wo die Sendefrequenz (die Relais-Eingabe) im unteren Teil des Frequenzbandes liegt und die Relais-Ausgabe (unsere Empfangsfrequenz) in der oberen Hälfte, würden wir vermutlich ein Reflektor-Design realisieren weil der Gewinn beim Senden besser ist und das Vorwärts/Rückwärtsverhältnis beim Empfang besser ist (vergleiche die beiden vorherigen Grafiken zu Gewinn und Vorwärts/Rückwärtsverhältnis).

Man beachte auch, dass der Optimierungs-Algorithmus Schwierigkeiten hat, überhaupt sinnvolle Lösungen für die Direktor-Variante zu finden. Nur bei einer handvoll Experimente war es überhaupt möglich, die obige Pareto-Front zu finden. Das Direktor-Design ist schmalbandiger als das Reflektor-Design und da das Stehwellenverhältnis ein Beschränkung (Constraint) ist, werden oft nur lokale Optima gefunden. Der größere Unterschied im Wertebereich von Gewinn- und Vorwärts/Rückwärtsverhältnis für das Direktor Design sagt uns ausserdem dass es schwieriger zu realisieren sein wird: Wenn die Dimensionen nicht exakt richtig getroffen werden wird die Antenne wohl weiter von den vorhergesagten Simulationsergebnissen abweichen. Das Reflektor-Design ist etwas toleranter in dieser Beziehung.

Als Funkamateur ist man hin und wieder mit der Herausforderung konfrontiert, eine Antenne an einen Transceiver über eine Übertragungsleitung anzuschließen. Oft ist dabei die Impedanz der Antenne unterschiedlich von der Impedanz der Übertragungsleitung und des Transceivers. Die Impedanz von Transceiver und einer typischen Coax Übertragungsleitung ist üblicherweise 50Ω im Amateurfunkbereich. Die Impendanz der Antenne ist je nach technischen und Gegebenheiten und Umgebungseinflüssen unterschiedlich.

Eine Übertragungsleitung transformiert je nach Länge die Impedanz der Antenne. Eine gut bekannte Formel wird z.B. von Chipman [1] S.134 Formel 7.15 angegeben:

In dieser Formel ist \(Z_d\) die Impedanz in einem Abstand von der Last \(d\) zur Antenne, \(Z_l\) ist die Impedanz an der Last (also der Antenne) und \(Z_0\) ist die characteristische Impedanz der Übertragungsleitung und des Transceivers, typischerweise 50Ω. \(\gamma\) ist der komplexe Übertragungskoeffizient, diesen kann man in den Real- und den Imaginärteil aufteilen, wobei dann \(\alpha\) die Dämpfung in Neper/m und \(\beta\) die Phasenkonstante ist, \(j\) ist die imaginäre Einheit (oft auch als \(i\) geschrieben aber in der Elektrotechnik meist als \(j\)):

Es wird manchmal behauptet, dass ein Kabel das Stehwellenverhältnis am Transceiver verbessern kann, weil es die Impedanz transformiert. Dies stimmt aber nur dann, wenn die characteristische Impedanz des Kabels unterschiedlich von der Impedanz des Transceivers ist (wenn wir annehmen dass das Kabel verlustfrei ist was in vielen Fällen von kurzen Kabeln gilt) was ich im folgenden zeigen werde.

Im verlustfreien Fall ist \(\alpha\) in der obigen Formel 0. Wir können \(\beta\) über die Frequenz und schließlich über die Wellenlänge \(\lambda\) ausdrücken:

und:

Die Frequenz \(f\) ist in Hz, \(c\) ist die Lichtgeschwindigkeit und \(\mathbb{VF}\) der Verkürzungsfaktor (im Englischen velocity factor) der Übertragungsleitung. Wenn wir die Entfernung von der Last \(d\) in Chipman's Formal als Vielfaches von \(\lambda\), \(l_\lambda\) ausdrücken, kürzen sich \(f\), \(c\) und \(\mathbb{VF}\), und wir bekommen für den verlustfreien Fall:

Der komplexe Reflexionskoeffizient \(\rho\) ist (siehe z.B. bei Chipman [1] 7.9 S.128):

wobei \(Z\) die Impedanz am Punkt der Leitung ist wo wir den Reflexionskoeffizienten wissen wollen. Daraus können wir das Stehwellenverhältnis berechnen (vgl. z.B. Chipman [1] 8.21 S.165) das ich hier mit \(S\) bezeichne:

Ein einfaches Python Programm (Python ist angenehm für solche Berechnungen weil es komplexe Zahlen unterstützt und freie Software ist) um obiges zu berechnen könnte wie folgt aussehen:

from math import e, pi
def impedance (z_load, l_lambda, z0 = 50.0):
    zl = z_load / z0
    ex = 2j * pi * l_lambda
    lp = e **  (ex) * (zl + 1)
    lm = e ** (-ex) * (zl - 1)
    return z0 * (lp + lm) / (lp - lm)

def vswr (z, z0 = 50.0):
    absrho = abs ((z - z0) / (z + z0))
    return (1 + absrho) / (1 - absrho)

Wenn wir das nun für einige Punkte berechnen, z.B. für eine Antenne mit 72Ω und für einige Vielfache von \(\lambda\) bekommen wir immer den selben Wert für das Stehwellenverhältnis:

Zu beweisen dass das Stehwellenverhältnis immer gleich ist, egal wie lang die Übertragungsleitung ist, wird an dieser Stelle als Hausaufgabe für den Leser gelassen. Ein Hinweise: Es genügt zu zeigen dass der Absolutbetrag von \(\rho\) gleich bleibt.

Der interessantere Fall ist aber nun, wenn wir Kabelverluste mit einbeziehen. Ich habe ein Stück Software geschrieben, das das Verhalten einer Coax Leitung aus den Herstellerangaben berechnen kann, eine Idee die schon vor langer Zeit von Frank Witt, AI1H [2] publiziert wurde. Die Implementierung ist Teil meines Open Source antenna-optimizer Projekts. und beinhaltet ein kleines Programm namens coaxmodel. Mit diesem kann die Impedanz (und Stehwellenverhältnis) für ein echtes Kabel berechnet werden. Die Implementierung enthält schon die Modelle einiger Kabel aber es ist recht einfach, neue dazuzugeben (siehe am Ende von coaxmodel.py). Zusätzlich kann man damit auch Anpassungen mit Hilfe einer Stichleitung berechnen: Wenn man ein Stück Übertragungsleitung parallel zur Speiseleitung in einem bestimmten Abstand zur Last anschließt (dieses Stück heisst dann Stichleitung) transformiert sich die Impedanz auf eine Weise dass der Generator (der Transceiver) eine Last von 50Ω sieht. Für obiges Beispiel würde es z.B. berechnen (Nur ein Teil der Ausgabe ist hier wiedergegeben, probieren Sie es selbst):

% coaxmodel -z 72 -f 435e6 -l .057 match
0.06 m at 435.00 MHz with 100 W applied
           Load impedance 72.000 +0.000j Ω
          Input impedance 46.857 -17.433j Ω
             VSWR at load 1.440
            VSWR at input 1.439
Inductive stub with open circuit at end:
            Stub attached 0.06246 m from load
              Stub length 0.20224 m
      Resulting impedance 50.00 -0.00j

Das verrät uns dass ein 5.7cm Stück Übertragungsleitung die 72Ω Impedanz an der Last (Antenne) in eine 46.86-17.43jΩ Impedanz am Eingang der Übertragungsleitung transformiert. Es wird auch klar dass sich das Stehwellenverhältnis durch Kabelverluste ganz leicht verbessert hat und dass man diesen Unterschied bei dieser Länge des Kabels vernachlässigen kann.

Wenn man nun eine 20.2cm Stichleitung von 50Ω mit einem offenen Ende parallel zur Speiseleitung im Abstand von 6.2cm von der Last anschließt, wird die Impedanz auf 50Ω transformiert mit einem Stehwellenverhältnis von 1:1.

Der Orange-Pi Zero ist ein beliebter Open Hardware Einplatinencomputer der unter Linux laufen kann. Er ist gut von neuen Linux Kerneln und dem U-Boot Bootloader unterstützt.

Neuere boards haben ein NOR-Flash das verwendet werden kann um den U-Boot Bootloader aufzuspielen. U-Boot kann aus den Sourcen mit folgenden Kommandos gebaut werden:

make orangepi_zero_defconfig
make

Dann kann mit den sunxi-tools (Debian Linux hat diese Tools als Paket seit etwa zwei Releases) der Bootloader ins NOR-Flash geladen werden. Zuerst wird der Orange-Pi USB-OTG Port (das ist der kleine µ-USB auf dem Board) mit einem Micro-USB Kabel mit einem Computer verbunden (am besten ein Debian Linux, mit anderen Systemen müssen Sie selbst rausfinden wie das geht). Der Orange-Pi darf keine SD-Karte eingesteckt haben. In meinen Experimenten war die Stromversorgung aus dem USB genug um mit folgendem Kommando den Bootloader ins NOR-Flash zu bekommen:

sunxi-fel -v -p spiflash-write 0 u-boot-sunxi-with-spl.bin

Die Datei u-boot-sunxi-with-spl.bin haben wir gerade mit obigen Kommandos gebaut. Bis hierher ist alles auf der sunxi.org Orange-Pi Zero Seite dokumentiert. Aber sobald der Bootloader mal geflasht ist, bootet der Orange-Pi nicht mehr in den FEL-Modus der für obiges Kommando gebraucht wird. Stattdessen startet der Bootloader aus dem NOR-Flash. Wenn jemals wieder eine neuere Version von U-Boot geflasht werden soll, muss der Orange-Pi wieder im FEL-Modus starten. Einige Methoden dazu sind auch auf der sunxi.org Seite dokumentiert. Leider ist die einfachste, dass man den RECOVERY-Kontakt auf Masse legt, was bei vielen Boards über einen Jumper möglich ist, beim Orange-Pi nicht so einfach weil der Anschluss über einen Pull-Up Widerstand (R 123) ohne Jumper fest angeschlossen ist. Zum Glück ist dieser Widerstand auf dem Board einfach zugänglich. Ich habe im Bild die Seite von R 123 auf dem Board mit dem rechten roten Pfeil markiert.

Diese Seite des Widerstands muss mit Masse verbunden werden. Ich verwende die Masse von der Debug-Schnittstelle (markiert mit dem linken roten Pfeil) weil alle anderen gut zugänglichen Masse-Anschlüsse direkt daneben einen +5V Kontakt haben. Wenn man versehentlich +5V mit irgendwas anderem auf dem Board kurzschließt kann man das Board zerstören. Daher ist der Masseanschluss an der Debug-Schnittstelle die sicherste Lösung. Wir verbinden Masse und den R 123 Kontakt, beide mit roten Pfeilen markiert, und schalten den Strom ein (z.B indem wir den OTG-USB verbinden). Dann ist zu überprüfen ob das Board wirklich im FEL-Modus ist mit dem Kommando:

sunxi-fel ver

Das Kommando druckt Versionsinformation zum Board oder eine Fehlermeldung wenn der FEL-Modus nicht erfolgreich gestartet wurde. Sobald das Board dann mal im FEL-Modus ist, kann ein neuer Bootloader aufgespielt werden.

Erfolgsmeldung vom obigen Kommando:

AWUSBFEX soc=00001680(H3) 00000001 ver=0001 44 08 scratchpad=00007e00 00000000 00000000

Fehlermeldung wenn der FEL-Modus nicht gestartet wurde:

ERROR: Allwinner USB FEL device not found!

[Edit 2021-10-25 Tippfehler gefixt, Danke Peter!]

Als ich vor kurzem Übertragungsleitungen für mein antenna-optimizer Projekt studiert habe, bin ich über eine Formel für den Q-Faktor eines Coax-Resonators von Frank Witt [1] gestolpert:

In dieser Formel ist \(F_0\) die Frequenz des Resonators in MHz, \(A\) is der Verlust in dB pro 100 ft, und VF ist der velocity factor (oder auf Deutsch "Verkürzungsfaktor") des Kabels. Die Formel war für einen \(\frac{\lambda}{4}\) Resonator angegeben. Ich habe mich über die Formel gewundert, weil ich dachte dass ein logarithmischer Wert für den Verlust eine Exponentiation bei der Berechnung des Q-Faktors erfordern sollte.

Wenn wir bei Wikipedia die Definition der Güte eines Schwingkreises nachschlagen bekommen wir:

Wobei \(E_s\) die gespeicherte Energie ist und \(E_d\) die während der Schwingung als Wärme verbrauchte Energie.

Wir wissen, dass der Verlustfaktor eines Kabels in dB Leistungsverluste definiert. Wenn der Verlust in dB pro 100m (wir verwenden natürlich metrische Einheiten) \(a\) ist, haben wir für den Verlust in dB:

Wobei \(l\) die Länge in Meter ist. Für einen \(\frac{\lambda}{4}\) Resonator bekommen wir:

Um die Verlustleistung als Faktor zu bekommen (statt in dB) bekommen wir:

Wir setzen

in die Formel ein, wobei \(c\) die Lichtgeschwindigkeit ist und \(f_0\) die Resonanzfrequenz in Hz:

Zurück zur Wikipedia-Formel die ja Energien benötigt müssten wir hier integrieren – aber weil beim Integrieren eines Verhältnisses wieder das selbe Verhältnis rauskommt machen wir so eine Art vereinfachende Integration wo wir uns nur überlegen müssen wie lang die von der Energie zurückgelegte Distanz ist. Die Wikipedia-Definition behandelt eine volle Periode, also \(\lambda\), nicht \(\frac{\lambda}{4}\). Und der Q-Faktor ist das Verhältnis von gespeicherter zu verlorener Energie. Wir haben also:

Wie wir sehen ist das \(Q\) des Resonators unabhängig vom Resonator-Typ, sei es ein \(\frac{\lambda}{4}\) oder \(\frac{\lambda}{2}\) Resonator.

Wenn wir Q-Faktoren für einige Kurzwellen-Frequenzen (in der Grafik sind die Frequenzen in MHz) gegen Verluste in dB auftragen, sehen wir dass obige Formel recht nahe bei der Näherungsformel von Witt [1] ist.

Plotten wir den Q-Faktor gegen die Frequenz (auch im Kurzwellen-Bereich) für typische Kabel, sehen wir auch dass der Fehler nicht sehr hoch ist, jedenfalls bei höheren Frequenzen.

Den relativen Fehler können wir auch darstellen, wieder für typische Kabel über den gesamten Kurzwellenbereich. Wir sehen, dass der Fehler recht hoch ist für niedrige Frequenzen und verlustreiche Kabel wie RG174.

Wir sehen also dass Witts Formel vermutlich eine Approximation ist, die recht gut für hohe Frequenzen und niedrige Verluste funktioniert. Die Frage ist aber offen: Woher kommt die Formel und woher kommt die magische Konstante die vermutlich alle physischen Konstanten in der Formel zusammenfasst?

Beim Studium von Übertragungsleitungen bin ich auch über ein älteres Buch gestolpert, das mal ein Universitäts-Lehrbuch war [2]. Auf S. 222 leitet Chipman eine Näherungsformel für \(Q\) her, die als vereinfachende Annahme ein niedriges \(\alpha\) (den Dämpfungskoeffizienten in Neper) voraussetzt. Chipman's Näherungsformel ist:

Hier ist \(\alpha\) der Dämpfungskoeffizient in Neper/m und \(\beta\) ist der Phasenfaktor in Radians pro Meter. Das Subscript \(r\) steht für Resonanz. Wir schreiben:

und

und Witts Verlust \(A\) pro 100 ft können wir auch schreiben (wir konvertieren Neper zu dB) als:

Wobei die Konstante 3.2808 der Konversionsfaktor m/ft ist. Lösen wir für \(\alpha_r\) und ersetzen \(\lambda\) und \(\alpha_r\) in Chipman's Formel bekommen wir:

Wobei das \(F_0\) die Frequenz \(f_0\) in MHz ist.

Wir sehen dass die Annahme von niedrigem \(\alpha\) in Chipman's (und Witt's) Formel für höhere Frequenzen und niedrige Verluste zutrifft: \(\alpha\) in Neper pro Meter ist ein konstanter Faktor wenn wir es in dB (pro 100m oder pro 100 ft) umrechnen. Dass die Näherung mit hohen Frequenzen besser wird, liegt daran, dass Kabelverluste typischerweise mit der Wurzel aus \(\lambda\) steigen, während \(\lambda\) invers proportional mit der Frequenz sinkt. Also hat z.B. ein \(\frac{\lambda}{4}\) Resonator höhere Verluste bei niedrigen Frequenzen.

In zwei älteren Artikeln in diesem Blog, einen zum Thema Zweiter SPI Chipselect für den Orange-Pi Zero, einen über das Hitachi HD44780 Text Anzeigemodul unter Linux habe ich darüber geschrieben, die Änderungen in den Linux Kernel zu bekommen.

Im Fall des Orange-Pi war das ein Bug-Fix des SPI-Treibers auf der Allwinner sun6i Architektur. Danke an diesem Punkt an den Autor Mirko, den Autor des Patches, der es mir erlaubt hat, den Patch in seinem Namen zu submitten. Der Patch ist im Linux Kernel kurz vor dem 5.13. Release. Weil er als Bug-Fix markiert war, wurde er auf einige Stable Release-Serien zurückportiert, bis zur 4.4 Stable Serie.

Im Fall des Hitachi Anzeigemodul war es ein Update der Dokumentation, die es Personen gestatten sollte, rauszufinden, wie man ein solches Display anschließt und die nötige Device-Tree Magie verwendet ohne Software ändern zu müssen. Dieser Patch wurde rechtzeitig für das 5.15 Release im Kernel akzeptiert.

WARNUNG: Im Folgenden werden ich beschreiben, wie man ein Netzteil ändert. Netzteile können hohe Spannungen führen – auch wenn der Stecker gezogen wurde weil in Kondensatoren noch Ladung gespeichert sein kann. In einigen Ländern darf nur eine geprüfte Fachkraft oder eine Person unter Aufsicht einer geprüften Fachkraft Geräte mit Netzspannung ändern. Du solltest also wissen was Du tust und dazu authorisiert sein.

PC Netzteile sind günstig und gut verfügbar aber sie geben die angegebenen Spannungen nur dann aus wenn der gezogene Strom bei jeder der unterschiedlichen Spannungen innerhalb der Minima und Maxima des Netzteils sind. Wenn man hohe Ströme (aber innerhalb der Spezifikation des Netzteils) nur bei einer einzigen Spannung zieht, sinkt die Spannung unter die in der Spezifikation angegebenen Mindestspannung.

Ein Beispiel ist das Heizbett meines 3D-Druckers: Er verwendete früher ein PC-Netzteil für das Heizbett. Das Heizbett zieht 12A und verwendet nur die 12V Stromversorgung. Das Resultat ist eine Spannung von etwa 10V wenn das Heizbett heizt.

Ein anderer Anwendungsfall ist die Versorgung von ARM-basierten Single-Board Computern (z.B. Raspberry-Pi or Orange-Pi) aus einer 5V Leitung. Wenn man dafür ein PC-Netzteil verwendet (ohne Strom aus der 12V Versorgung zu benötigen) kann die nominelle 5V Spannung unter den Bereich sinken wo der Single-Board Computer noch zuverlässig funktioniert.

Ein drittes Beispiel ist die Stromversorgunge von Funkgeräten eines Funkamateurs: Diese Geräte liefern üblicherweise nicht die volle Sendeleistung wenn sie mit 12V oder weniger versorgt werden, sie brauchen typischerweise 13.6-13.8V für volle Sendeleistung.

In allen diesen Fällen wäre eine Modifikation des Netzteils so dass die ausgewählte Spannung stabil bleibt oder wo es sogar möglich ist, die ausgewählte Spannung leicht zu verändern (von 12V auf 13.8V für Funkamateure), sehr nett. Wie können wir das erreichen?

Viele PC-Netzteile haben als Spannungsregler die integrierten Schaltkreise TL494 oder KA7500 (diese sind Pin-Kompatibel) verbaut. Wenn unser Netzteil einen davon hat kann man es üblicherweise modifizieren um eines der oben genannten Zwecke zu erreichen.

Ein Schaltungsdetail solcher Netzgeräte ist ein Rückkopplungszweig der die 5V und 12V Spannungen zum Regler-IC führt. Auf Dan's PC power supply page findet man viele Schaltungen von PC-Netzteilen. Nehmen wir das zweite in der Liste von TL494 und KA7500 basierten Geräten. Es hat einige parallele Widerstände von pin 1 des TL494 nach Masse und einen 27kΩ-Widerstand von 12V an pin 1 sowie einen 4.7kΩ-Widerstand von 5V zum selben Pin.

Wir können die Spannungsregelung verändern, indem wir die Rückkopplungs Widerstände ändern. Es sei angemerkt, dass üblicherweise jedes Netzteil unterschiedliche Widerstände nach Masse und unterschiedliche Rückkopplungs Widerstände von 5V und 12V hat. Als Beispiel ändern wir nun die Rückkopplungs-Widerstände so dass das Netzteil stabile 5V liefert ohne dass wir uns um die 12V Spannung kümmern.

WARNUNG: Wenn man ein Netzteil für stabile 5V oder 12V Versorgung modifiziert hat, sind die anderen Spannungen nicht mehr stabil und können zu hoch für die Nutzung in einem PC werden. Man sollte niemals ein modifiziertes Netzteil in einem PC einsetzen.

Der erste Schritt ist mal, die beiden Rückkopplungs Widerstände im Netzteil zu finden. Einmal gefunden verifizieren wir dass die Seite die nicht am Pin 1 des Reglers liegt mit 0Ω mit dem 5V bzw. 12V Ausgang verbunden ist. Dann löten wir beide Widerstände aus. Bevor wir jetzt den neuen Widerstand zwischen Pin 1 und 5V berechnen, messen wir den Widerstand von Pin 1 nach Masse: Weil wir ja nun die beiden Widerstände nach 12V und 5V ausgelötet haben, kann der Widerstand nach Masse störungsfrei gemessen werden. Es ist an dieser Stelle sinnvoll, sicher zu sein, dass der gemessene Widerstandswert und der berechnete aus den drei parallel geschalteten Widerständen übereinstimmen: Im Beispiel-Schaltplan haben wir 100kΩ, 390kΩ und 10kΩ parallelgeschaltet, die gemessen den Wert haben:

Als ich neulich ein Netzteil umgebaut habe, waren die drei Widerständen nach Masse 470kΩ, 100kΩ und was ich dachte dass 8.9kΩ wären. Ich hatte die Farben des letzten Widerstands als Grau-Weiss-Schwarz-Braun-Braun interpretiert. Als ich die drei parallelen Widerstände gemessen habe war das Ergebnis 4.61kΩ statt der erwarteten 8033Ω. Es stellte sich heraus (nach genauem Ansehen des Widerstands im Sonnenlicht) dass das was ich als Grau eingestuft hatte eher gelblich war. Der Widerstand hatte also in Wirklichkeit 4.9kΩ und der berechnete Gesamtwiderstand war 4625Ω.

Um ein Netzteil nur die 5V regeln zu lassen verbinden wir einen neuen Widerstand von Pin 1 des Regler-ICs mit 5V und lassen die 12V Rückkopplung unbeschaltet. Aber wie wählen wir den neuen Widerstand? Um den zu berechnen müssen wir ein Gleichungssystem lösen. Wir wissen vom Ohmschen Gesetz die Verhältnisse von Strömen, Spannungen und Widerständen. Von Kirchhoff wissen wir, dass die Summe des Stroms durch den 5V Widerstand und durch den 12V Widerstand gleich dem Strom durch die Massewiderstände sein muss. Diese Verhältnisse sind in einem Maxima Spreadsheet zusammengefasst.

Wir berechnen die Referenzspannung an Pin 1 wenn sowohl der Widerstand von 5V als auch der von 12V angeschlossen sind. Dann wählen wir einen neuen Widerstand der nur an 5V angeschlossen ist so, dass sich die selbe Referenzspannung ergibt.

Zum Beispiel in obigem Schaltplan bekommen wir ziemlich genau 1800Ω für R_new, den neuen Widerstand. Für das Netzteil, das ich vor kurzem modifiziert habe, habe ich schon die Widerstände nach Masse angegeben. Der Widerstand nach 12V war 39kΩ und der Widerstand nach 5V war 9.1kΩ. Der resultierende neue Widerstand R_new für dieses Netzteil war 4865Ω was durch Serienschaltung von einem 4.7kΩ und einem 150Ω Widerstand erreicht wurde, damit ist die 5V Ausgangsspannung genau genug erreicht. Diese Berechnung findet sich als zweites Beispiel im Spreadsheet.

Noch ein Wort zur Vorsicht: Wenn man ein Netzteil für stabile 5V Versorgung modifiziert oder für eine höhere Spannung am 12V Ausgang sollte man sich bewusst sein, dass die meisten PC-Netzteile im 12V-Zweig Kondensatoren haben die für 16V spezifiziert sind. Wenn man dann hohe Ströme bei 5V zieht, kann die Spannung am 12V Ausgang zu hoch für diese Kondensatoren werden. Um auf der sicheren Seite zu sein, sollte man diese Kondensatoren durch 25V-Typen ersetzen.

Um die 12V Stromversorgung zu fixieren wird im Prinzip die selbe Prozedur wie für 5V verwendet, nur dass wir den 12V Rückkopplungs-Widerstand anschließen und den 5V Widerstand unbeschaltet lassen. Wie man den Widerstand für 12V berechnet ist Hausaufgabe.

Ich habe vor kurzem einem Kunden einen Link zu einem Firewall Image (für den Turris MOX Router mit einer Variante von OpenWRT) auf meinem eigenen Webserver geschickt. Das Image enthielt Key-Material für eine OpenVPN Verbindung. Die Datei war in einem versteckten Verzeichnis auf meinem Projekt-Webserver. Ich habe genau geschaut, ob es noch andere Downloads gab, zusätzlich zu dem meines Kunden.

Ich bin mir bewusst, dass es nicht die beste Sicherheitspraxis ist, Key-Material über einen unsicheren Kanal zu übertragen. Und am Ende musste ich das VPN Key-Material das im Image war revoken und meinem Kunden über einen sicheren Kanal einen neuen Schlüssel zukommen lassen.

Nun, ich hatte schon erwähnt, dass ich die Downloads beobachtet hatte. Etwa eine Stunde (!) nachdem mein Kunde das Image geholt hatte (um genau zu sein um 21/Mar/2021:17:35:50) wurde von einer anderen IP darauf zugegriffen:

77.74.177.4 - - [21/Mar/2021:18:43:51 +0100] "GET /turris-image-XXXXXXX.zip HTTP/1.1" 200 77244886 "-" "Mozilla/5.0 (Windows NT 10.0; Win64; x64) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/81.0.4044.92 Safari/537.36"

Wenn man diese IP über whois sucht findet man:

> whois 77.74.177.4
% This is the RIPE Database query service.
...
netname:        KL-NET3
descr:          Kaspersky Lab Internet
country:        RU
...
source:         RIPE
organisation:   ORG-KL28-RIPE
org-name:       Kaspersky Lab AO
country:        RU

Mein Kunde hat die Kaspersky Antivirus-Software installiert. Der Link wurde also vermutlich an Kaspersky über diese installierte Software weitergegeben. Es kann ja einerseits sein, dass der Grund, warum Kaspersky das Image heruntergeladen hat ein harmloser war, möglicherweise um ein Service zu erbringen (wie z.B. der Scan auf Viren) aber in meinem Fall hat das bedeutet dass nicht öffentliche Informationen Dritten bekannt wurden. Auf der anderen Seite könnte es sein, dass diese Informationen auch für andere Zwecke verwendet werden – wir wissen es nicht.

Also beachten Sie dass Ihr Antivirus-Produkt Ihnen beim Download im Web über die Schulter schaut.

Ich unterrichte an der Fachhochschule Burgenland in Eisenstadt (Österreich). Dort hatten wir vor kurzem eine Laborübung (die zwar im Labor stattfand aber alle Studenten arbeiteten von zuhause auf den Laborrechnern aus Covid-Gründen) wo die Aufgabe war, mit libvirt eine laufende virtuelle Maschine auf einen anderen Server zu migrieren (wir verwenden die Kommandozeile und virsh).

Bei einer von mehreren Gruppen – alle mit identischen Debian Installationen – schlug die Migration mit einer Fehlermeldung fehl. Das Migrations-Kommando war:

virsh -c qemu+ssh://root@primary/system migrate --live --unsafe \
    debian-1 qemu+ssh://root@secondary/system

Für die Laborübung verwenden wir NFS weil ein besseres verteiltes Filesystem zu viel Zeit kosten würde, daher verwenden wir die --unsafe Option bei der Migration. Die folgende Fehlermeldung war das Resultat (die Meldung ist in mehrere Zeilen zerlegt, die Meldung ist normalerweise alles in einer Zeile):

error: internal error: Process exited prior to exec:
libvirt:  error : unable to set AppArmor profile
'libvirt-d22db7ca-50ca-43bd-b6da-1ccecf5a83e7' for '/usr/bin/kvm':
No such file or directory

Es stellte sich dann heraus, dass es diese Gruppe geschafft hatte, die /var Partition mit Log-Dateien zu füllen. Aber auch nach Aufräumen kam noch die gleiche Fehlermeldung. Das Gefühl sagte, dass hier von AppArmor und/oder libvirt dynamisch erzeugte Dateien nicht erzeugt werden konnten und dass dies der Grund für den Fehlschlag war. Ausserdem stellte sich heraus, dass einige AppArmor Dateien die auf der ersten Maschine korrekt installiert waren auf der zweiten Maschine fehlten.

Eine Neuinstallation von AppArmor und den zugehörigen Dateien mit apt-get mit der Option --reinstall funktionierte nicht, die fehlenden Konfigurationdateien in /etc/apparmor.d wurden nicht neu erzeugt. Daher war deinstallieren der Pakete mit dem purge Kommando (dieses entfernt auch die Konfigurationdateien) und dann Neuinstallation der Ausweg um die fehlenden AppArmor Dateien zu bekommen und so die Migration schlussendlich durchzuführen. Ich habe bis jetzt keine Ahnung, welche Dateien gefehlt haben.

Wenn man nach der obigen Fehlermeldung googled, findet man einen Debian Bug-Report wo eine der dynamisch erzeugten Dateien in /etc/apparmor.d/libvirt die Länge Null hatte. Dies war jedoch nicht das Problem in unserem Fall, zeigt aber dass AppArmor nicht besonders sorgfältig die Fehler prüft, z.B. wenn das Dateisystem voll ist. Es gibt also vermutlich noch andere Dateien die dynamisch erzeugt werden die in unserem Fall das Problem waren.

Die folgende Abfolge von Deinstallations und Re-Installations Kommandos hat das Problem in unserem Fall behoben. Es sei darauf hingewiesen dass das Entfernen der beiden Dateien wie im Debian Bug-Report das Problem in unserem Fall nicht gelöst hat:

dpkg --purge apparmor-utils apparmor-profiles
dpkg --purge apparmor
rm -rf /var/cache/apparmor
apt-get install apparmor apparmor-utils apparmor-profiles
dpkg --purge libvirt-daemon-system
apt-get install libvirt-daemon-system
systemctl restart libvirtd.service
systemctl restart virtlogd.service
systemctl restart virtlogd.socket

Ich bin nicht sicher dass man alle Services wirklich neu starten muss, aber es gab ein Problem dass libvirt nicht auf den virtlog Socket verbinden konnte und das ließ sich durch ein Restart von virtlog.{service,socket} beheben.

Der bekannte DNS server bind erlaubt Konfigurationen die es ermöglichen, dass clients ihre DNS Einträge selbst verändern können. Weil einige öffentliche dynamische DNS Services zu einem Bezahlmodell gewechselt sind und weil ich sowieso meinen eigenen Mail- und Webserver bei einem Hoster betreibe, suchte ich nach einer Möglichkeit, meinen eigenen dynamischen DNS Server zu verwenden. Das liegt schon ein paar Jahre zurück, aber weil das von mir damals verwendete Howto vom Netz (oder zumindest aus meiner Google-Bubble) verschwunden ist, dokumentiere ich hier wie ich das gemacht habe.

Die Software läuft bei mir unter Debian Buster zur Zeit dieses Blog-Eintrags, die Details können sich also bei anderen Systemen ändern. In den folgenden Beispielen nenne ich die Subdomain für die dynamischen DNS Einträge dyn.example.com.

Die Konfigurations-Datei von bind braucht ein zusätzliches include um die Konfigurations-Datei für die dynamische Domain einzubinden. In meiner Konfiguration heisst diese Datei named.conf.handedited. In dieser Datei braucht es einen Entrag für jeden dynamischen DNS Client wie folgt:

zone "dyn.example.com" {
        type master;
        allow-transfer {none;};
        file "/etc/bind/slave/pri.dyn.example.com";
        update-policy {
            grant h1.dyn.example.com. name h1.dyn.example.com. A TXT;
            grant h2.dyn.example.com. name h2.dyn.example.com. A TXT;
            [...]
        };
};

In diesem Beispiel dürfen die Hosts h1 und h2 (und möglicherweise weitere) ihre eigenen DNS Einträge ändern. Ich erlaube hier dass sie den A und TXT Record ändern. Für IPv6 möchte man hier noch AAAA dazugeben.

Die Konfigurations-Datei /etc/bind/slave/pri.dyn.example.com enthält dann:

dyn.example.com         IN SOA  ns1.example.com. admin.example.com. (
                                2020080100 ; serial
                                120      ; refresh (2 minutes)
                                120      ; retry (2 minutes)
                                120      ; expire (2 minutes)
                                120      ; minimum (2 minutes)
                                )
                        NS      ns1.example.com.
h1                      A       127.0.0.1
                        KEY     512 3 10 (
                                AwEAAdEvnGmGO4ku+xms4w1c5RWh5BvugiZ4ty9tkIes
                                <more gibberish lines>
                                ); alg = RSASHA512 ; key id = <number>

Die Einträge in spitzen Klammern sind Kommentare und sollten durch die korrekten Werte in der Zielinstallation ersetzt werden. Die Einträge A und KEY werden von Hand für jeden neuen Host der seine eigene IP-Adresse setzen können soll eingetragen. Der KEY ist der öffentliche Schlüssel (public key) der weiter unten erzeugt wird. Nach meiner Erfahrung braucht es den A-Eintrag damit das ganze funktioniert. Ich setze hier eine localhost Adresse weil der Client diese später sowieso überschreiben wird. Es ist üblich die Admin Email-Adresse (wo @ durch einen Punkt ersetzt ist) im SOA-Eintrag an die Stelle zu setzen wo ich admin.example.com. eingetragen habe.

Um einen neuen Client Host anzulegen geht man wie folgt vor:

• Erzeugen eines Schlüsselpaares (öffentlicher / privater Schlüssel, public/private key), bevorzugt passiert das beim Client und dieser sendet nur den öffentlichen Schlüssel an den DNS-Administrator um Sicherheitsprobleme bei der Schlüssel-Übermittlung zu vermeiden:

  dnssec-keygen -T key -a RSASHA512 -b 2048 -n HOST newhost.dyn.example.com

• Das erzeugt einen privaten und einen öffentlichen Schlüssel. Zu beachten: Der Client braucht beide Schlüssel, sowohl den öffentlichen als auch den privaten, obwohl nur der private Schlüssel dem dynamischen DNS Client übergeben wird!

• Das letzte Mal als ich einen neuen Schlüssel erzeugt habe, konnte das Kommando keine Schlüssel mit mehr als 2048 bits erzeugen, obwohl der verwendete Hash-Algorithmus SHA2 modern ist und eine große Bitlänge unterstützt.

• Damit bind seine Datenbank auf eine Datei schreibt (und man diese editieren darf) muss man bind für diese Domain einfrieren:

  rndc freeze dyn.example.com

• Jetzt darf man das Konfigurationsfile ändern und einen neuen Absatz für einen neuen Host eintragen. Nicht vergessen die serial Nummer zu erhöhen:

  $EDITOR /etc/bind/slave/pri.dyn.example.com

• Dann nicht vergessen, die Domain wieder aufzutauen:

  rndc unfreeze dyn.example.com

• Und schließlich nicht vergessen, dem neuen Host die nötigen Berechtigungen in named.conf.handedited zu geben.

• Zuletzt muss man wohl dem bind ein reload geben:

  systemctl reload bind9.service

Auf der Client-Seite heisst das Programm um bind mitzuteilen dass sich die IP-Adresse des Client geändert hat nsupdate. Man findet diese Programm für viele Betriebssysteme.

Ich verwende ein simples Script am Client das die Änderung der dynamischen IP Adresse bemerkt und eine Adressänderung bei bind anstößt wenn sich die IP Adresse geändert hat. Nachdem wir unseren eigenen DNS-Server betreiben sind die Chancen groß, dass es dort auch einen eigenen Webserver gibt. Das folgende einfache Script erlaubt es dem Client, seine eigene IP-Adresse rauszufinden (Clients sind oft hinter einer NAT Firewall und wir wollen ja nicht wieder auf ein anderes öffentliches Service angewiesen sein, wenn wir gerade öffentliche dynamische DNS Services losgeworden sind, oder?):

#!/bin/sh
echo Content-Type: text/plain
echo ""
echo $REMOTE_ADDR

Dieses Script installiert man in ein cgi-bin Verzeichnis auf einem Webserver. Es liefert dem anfragenden Client seine eigene IP-Adresse (in Text Format) zurück. Das script heisst bei mir ip.cgi und ist dann unter der URL http://example.com/cgi-bin/ip.cgi in unserem Beispiel verfügbar. Die URL muss dann unten im Client-Script geändert werden.

Mein bind Script (einige Variablen müssen geändert werden) schaut aus wie folgt (bitte beachten: Das Script geht davon aus dass obiges IP-Adressen Script auf der Domain example.com läuft, das muss natürlich auch geändert werden):

#!/bin/sh
ZONE=dyn.example.com
DOMAIN=h1.dyn.example.com
DNSKEY=/etc/nsupdate/Kh1.dyn.example.com.+010+04711.private
NS="ns1.example.com"

registered=$(host $DOMAIN $NS 2> /dev/null | grep 'has address' | tail -n1 | cut -d' '  -f4)
current=$(wget -q -O- http://example.com/cgi-bin/ip.cgi)
[ -n "$current" \
-a "(" "$current" != "$registered" ")" \
] && {
 nsupdate -d -v -k $DNSKEY << EOF
server $NS
zone $ZONE
update delete $DOMAIN A
update add $DOMAIN 60 A $current
send
EOF
 logger -t dyndns -p daemon.notice "Updated dyndns: $registered -> $current"
} > /dev/null 2>&1

exit 0

Es sei nochmal darauf hingewiesen, dass der private Schlüssel (in obigem Beispiel in /etc/nsupdate/Kh1.dyn.example.com.+010+04711.private nicht ausreicht, das Programm nsupdate braucht auch den öffentlichen Schlüssel im selben Verzeichnis wie das des privaten Schlüssels.

Für ein Projekt verwende ich ein Text Anzeigmodul mit dem Hitachi HD44780 Chip. Diese Displays gibt es in verschiedenen Größen, üblich sind 2 Zeilen mit 16 Zeichen oder 4 Zeilen mit 20 Zeichen. Die letztere Variante wird auch unter dem Namen 2004a vertrieben. Diese Displays arbeiten mit 5V. Weil heutzutage die meisten Microcontroller und CPUs mit 3.3V oder weniger betrieben werden, wird so ein Display oft an einen I²C-Bus über eine I/O Erweiterung (ein sogenannter GPIO Extender) angeschlossen, die meisten davon mit einem PCF8574 Chip. Man kann die Displays und GPIO Extender separat oder zusammen kaufen, auflöten muss man das extender-Modul in jedem Fall selbst.

Das korrekte Vorgehen, so ein Display an einen 3.3V I²C Bus anzuschließen wäre über einen Pegelwandler. Es gibt aber einen Hardware-Hack wo man einfach die Pull-Up Widerstände auf dem PCF8574 Board entfernt (diese hängen direkt an +5V). Diese Änderung macht den GPIO Extender kompatibel mit 3.3V Installationen: Der im Datenblatt des PCF8574 angegebene minimale High-Pegel ist zwar 0.7 * VCC (was 3.5V bedeuten würde), in der Praxis funktioniert er aber einwandfrei mit 3.3V. Es sei darauf hingewiesen, dass die Nummern der Widerstände wie im Hardware-Hack angegeben (R5/R6) je nach Variante des PCF8574 Boards variieren. Ich habe die Nummern R8 und R9 gesehen sowie auch gar keine Beschriftung der Widerstände. Die Widerstände sind 4.7 kΩ, üblicherweise beschriftet mit 472 in der SMD Variante.

Dann habe ich untersucht, ob es einen Linux-Treiber für diese Displays gibt und habe einen in drivers/auxdisplay/hd44780.c im Kernel gefunden. Auf den ersten Blick schaut es so aus als ob dieser Treiber die Ansteuerung mit I²C über den PCF8574 I/O Extender nicht unterstützt. Also habe ich einen Treiber geschrieben und als Kernel-Patch eingereicht.

In der Diskussion (danke an Geert) hat sich dann herausgestellt, dass es einen Treiber für den PCF8574 im Kernel gibt (das hatte ich schon gesehen) und dass man den HD44780 Treiber mit der nötigen Device-Tree Magie so konfigurieren kann dass der PCF8574 Treiber für den I/O Extender verwendet wird. Die folgenden Device-Tree Beschwörungsformeln definieren ein Overlay das den PCF8574 mit seiner Standard I²C-Adress 0x27 konfiguriert und diesen dann für die I/Os des hd44780 Treibers verwendet:

// Note that on most boards another fragment must enable the I2C-1 Bus

/dts-v1/;
/plugin/;

/ {
        fragment@0 {
                target = <&i2c1>;
                __overlay__ {
                        #address-cells = <1>;
                        #size-cells = <0>;

                        pcf8574: pcf8574@27 {
                                compatible = "nxp,pcf8574";
                                reg = <0x27>;
                                gpio-controller;
                                #gpio-cells = <2>;
                        };

                };
        };

        fragment@1 {
                target-path = "/";
                __overlay__ {
                        hd44780 {
                                compatible = "hit,hd44780";
                                display-height-chars = <2>;
                                display-width-chars  = <16>;
                                data-gpios = <&pcf8574 4 0>,
                                             <&pcf8574 5 0>,
                                             <&pcf8574 6 0>,
                                             <&pcf8574 7 0>;
                                enable-gpios = <&pcf8574 2 0>;
                                rs-gpios = <&pcf8574 0 0>;
                                rw-gpios = <&pcf8574 1 0>;
                                backlight-gpios = <&pcf8574 3 0>;
                        };
                };
        };
};

Weil das nicht nur für mich nicht offensichtlich ist (in meiner Nachforschung habe ich mindestens zwei Linux-Treiber Implementierungen für die Kombination von HD44780 und PCF8574 ausserhalb des Linux-Kernels gefunden) habe ich einen Dokumentations-Patch eingereicht um das besser zu dokumentieren für Menschen die auch einen Linux-Treiber für diese Kombination suchen.

Es sei noch angemerkt, dass der Treiber für das Display Escape-Sequenzen verwendet um Spezialfunktionen des Displays (z.B. Ein/Ausschalten der Hintergrundbeleuchtung, löschen des Bildschirms, oder Benutzerdefinierte Bitmap-Zeichen) anzusteuern. Ich glaube diese sind nur im Source-Code in drivers/auxdisplay/charlcd.c dokumentiert.