Einige Leser hier wissen dass ich PGApack, ein Paket für Genetische Algorithmen, zusammen mit PGApy einer Python Bibliothek pflege (maintaine). Vor kurzem kam die Frage auf, warum PGApack wenn eine Selektionsmethode verwendet wird die proportional zur Fitness selektiert (Fitness Proportionate Selection), im englischen auch als Roulette-Rad Selektion bezeichnet, mit einem Fehler aussteigt weil es einen Fitness-Wert nicht normalisieren kann. Im folgenden werde ich kurz von proportionaler Selektion schreiben.

In PGApack definieren wir als Anwenderin eine Reelle Bewertungsfunktion (die für jedes Individuum aufgerufen wird). Ausserdem definieren wir ob diese Bewertung minimiert oder maximiert wird (wir legen die Optimierungsrichtung fest).

Bei proportionaler Selektion muss diese Bewertung auf positive Werte abgebildet werden so dass jeder Bewertung ein Teil des Roulette-Rades zugewiesen wird. Wenn minimiert wird sind kleine Werte besser und müssen einen größeren Bereich des Roulette-Rades bekommen so dass die Wahrscheinlichkeit der Selektion höher ist. Wir müssen also die Bewertungsfunktion auf eine nicht-negative monoton steigende Fitness abbilden. Bei einem Minimierungsproblem berechnen wir die maximale (schlechteste) Bewertung und bilden dann die Differenz dieses Maximums mit der Bewertung des Individuums (nach einer Skalierung des Maximums so dass kein Fitnesswert negativ wird):

wobei \(F\) die Fitness des aktuellen Individuums ist, \(E_{max}\) das Maximum aller Bewertungen der aktuellen Generation und \(E\) die Bewertung des Individuums.

Wenn sich nun die Bewertungen um mehrere Größenordnungen unterscheiden kann es vorkommen, dass die Fitness zu \(E_{max}\) wird, für viele (unterschiedliche) Individuen. Ich nenne das einen Überlauf (overflow), vielleicht nicht der beste Name dafür.

Der Überlauf passiert wenn \(E_{max}\) groß ist verglichen mit der aktuellen Bewertung \(E\) so dass die obige Differenz \(E_{max}\) wird (die Subtraktion von \(E\) also keine Wirkung hat) Im Code checken wir diese Bedingung:

if (cmax == cmax - evalue && evalue != 0)

Die Bedingung ist erfüllt wenn die Subtraktion von \(E\) von \(E_{max}\) \(E_{max}\) nicht verändert obwohl \(E\) ungleich Null ist. \(E\) ist so klein gegenüber \(E_{max}\) dass der Datentyp double den Unterschied nicht repräsentieren kann. Das passiert wenn die Einheit der letzten Stelle (units in the last place von Goldberg (nicht dem Goldberg der das Genetische Algorithmen Buch geschrieben hat soweit ich weiss) auch ulps genannt) der Mantisse größer ist als der Wert der subtrahiert wird [1].

In unserem Beispiel \(E_{max} = 1.077688 * 10^{22}\) und die Bewertung bei der das schiefging war \(E = 10000\). Ein IEEE 754 Fließkomma-Wert doppelter Genauigkeit (double) hat 53 bit Mantisse die damit Zahlen bis \(2^{54} - 1 = 18014398509481983\) darstellen kann, also etwa \(1.8 * 10^{16}\). Man sieht dass die Zahl 10000 gerade unterhalb des oben erwähnten ulps ist. Wir können das in Python ausprobieren (das für Fließkommazahlen double verwendet):

>>> 1.077688e22 - 10000 == 1.077688e22
True

Warum machen wir diesen Check im Programm? Würde die Suche bei einem solchen Überlauf (oder wie auch immer wir das nennen wollen) weiterlaufen, würde der Algorithmus viele verschiedene Bewertungen auf die gleiche Fitness abbilden. Der Genetische Algorithmus könnte also diese Individuen nicht unterscheiden.

Was können wir tun wenn dieser Fehler auftritt?

Die kurze Antwort: Einen anderen Selektionsmechanismus verwenden. Es gibt einen Grund, warum proportionale Selektion nicht die Standardeinstellung in PGApack ist.

Proportionale Selektion (Fitness proportionate selection) hat noch andere Probleme. Sie hat zu großen Selektionsdruck am Anfang zu wenig gegen Ende der Optimierung (auch erwähnt im obigen Wikipedia Artikel, aber Vorsicht, ich habe Teile davon geschrieben).

Blickle and Thiele [2] haben eine mathematische Analyse von unterschiedlichen Selektions-Algorithmen publiziert und gezeigt dass proportionale Selektion typischerweise keine gute Idee ist (proportionale Selektion war historisch der erste Selektionsmechanismus in der Literatur und war ausführlich in Goldbergs (der andere Goldberg) Buch [3] beschrieben und ist vielleicht deshalb heute noch manchmal in Verwendung). Es sei darauf hingewiese dass Blickle und Thiele in einem früheren Report [4] direkter waren was die Beurteilung von proportionaler Selektion betrifft (meine Übersetzung): "Alle unerwünschten Eigenschaften zusammen führten uns zu dem Schluss dass proportionale Selektion ein sehr ungeeigneter Selektionsmechanismus ist. Informell könnten wir sagen dass der einzige Vorteil von proportionaler Selektion ist, dass es so schwierig ist die Nachteile zu beweisen" ([4], S. 42), in der Endfassung im veröffentlichten Artikel waren sie dann nicht mehr so deutlich :-)

Wir sehen in obigem Beispiel: Wir haben sehr große Unterschiede zwischen guten und schlechten Bewertungen (eben so groß dass die Fitness nicht eindeutig berechnet werden kann, s.o.). Wenn man dafür proportionale Selektion verwendet, werden sehr gute Individuen mit zu großer Wahrscheinlichkeit selektiert was zu verfrühter Konvergenz (premature convergence) führt.

Zum Schluss all dieser Ausführungen: Wenn wir Optimierungen mit Fließkomma-Repräsentationen durchführen (diese werden durch double Datentypen in PGApack repräsentiert) sollten wir Differential Evolution ausprobieren [5], [6], [7]. Zumindest in meinen Experimenten mit Antennen-Optimierung [8] sind die Resultate damit deutlich besser als mit standard Genetischen Algorithmen was auch von verschiedenen Praktikern bestätigt wird [7]. Beispiele dazu finden sich in examples/deb/optimize.c oder examples/mgh/testprogde.c in PGApack.

Der Parameter PGASetDECrossoverProb ist kritisch. Für Probleme wo die Dimensionen nicht einzeln optimierbar sind, sollte der Wert nahe bei, aber nicht gleich 1 sein.

Für mein pymininec Projekt (eine Re-Implementierung des Original-Mininec [1] in Python, siehe die Beschreibung dort wie es möglich war, 40 Jahre alten Basic-code zu Reverse-Engineeren) hatte ich eine Möglichkeit gebraucht, die Resultate graphisch darzustellen. Daher hatte ich zuerst ein Visualisierungswerkzeug in pymininec inkludiert.

Nachdem ich dann aber auf die Schnelle einen Parser für die Ausgabe von nec2c geschrieben hatte, stellte sich heraus, dass das Programm auch allein nützlich ist. Daher habe ich es als eigenes Projekt plot-antenna genannt.

NEC (vielleicht übersetzbar mit numerischer elektromagnetischer Code) wurde ursprünglich am Lawrence Livermore National Laboratory in Fortran entwickelt. Bis Version 2 ist das freie Software, spätere Versionen sind nicht frei (inzwischen ist NEC bei Version 5). Neoklis Kyriazis hat die Fortran Version von NEC-2 nach C übersetzt und das Resultat nec2c genannt. Er hat einige Optimierungen vorgenommen, z.B. das ursprünglich separate Programm SOMNEC (um ein Sommerfeld/Norton Erdungsmodell zu berechnen) integriert und einige Limitierungen des ursprünglichen Fortran-Codes beseitigt. Das Programm nec2c ist eines von wenigen Open Source Antennen-Modellierungsprogrammen. Es ist ein Kommandozeilen-Programm das aus der Beschreibung einer Antenne eine Ausgabedatei mit vielen Tabellen berechnet. Es gibt andere Programme wie xnecview die mit dieser Ausgabedatei eine Antennen-Visualisierung erzeugen können.

An dieser Stelle ist zu bemerken, dass ich keine offizielle Webseite von nec2c gefunden habe. Das Programm ist in Debian und Ubuntu (Ubuntu sucht auch nach der offiziellen Upstream-Version) enthalten und es scheint die ursprüngliche Version war mal auf Google Code gehostet. Es gibt eine Version auf Github die auf eine andere Version auf Github verweist. Die Software scheint heutzutage nicht gewartet zu werden – kein großes Problem weil auch NEC in Version 2 seit ein paar Dekaden keine Updates mehr bekommt.

Zurück zu plot-antenna: Ursprünglich hatte das Programm nur einen Parser für die Ausgabe von pymininec (und für das Original Mininec [1] Basic-Programm). Später habe ich dann einen Parser für NEC hinzugefügt. Die derzeitigen Parser sind wahrscheinlich nicht sehr robust, funktionieren aber für meine Zwecke.

Die erste Version verwendet Matplotlib für die Grafikausgabe und diese Variante ist immer noch unterstützt. Urprünglich hatte ich Azimuth- und Elevationsdiagramme, sowie eine 3D-Anzeige implementiert.

Kürzlich, nachdem ich einige Zeit vorher Plotly entdeckt hatte, habe ich HTML/Javascript Ausgabe mithilfe von Plotly hinzugefügt. Die 3D Möglichkeiten von Plotly sind deutlich besser als die von Matplotlib – sogar mit 1 Grad Auflösung bei den Antennen-Winkeln (Azimuth/Elevation), also 180 * 360 3D Punkten, funktioniert das Display im Browser (Firefox). Mit der 3D Variante von Matplotlib muss 5 Grad Auflösung verwendet werden (36 * 72 3D Punkte), sonst ist die Anzeige sehr ruckelig. Mit der folgenden Grafik kann selbst damit experimentiert werden (kann auch in einem vollen Browserfenster dargestellt werden):

Nicht zu reden von Zoom: Das funktioniert in Plotly ausgezeichnet (mit dem Scroll-Rad der Maus in obiger Grafik) und scheint in Matplotlib garnicht implementiert zu sein.

In der Plotly Version zeichnen wir die Visualisierung für alle Frequenzen in eine Grafik. Für die 3D-Ansicht sind alle Visualisierungen bis auf die der gerade selektierten Frequenz versteckt. Über die Frequenz-Legende auf der rechten Seite kann die jeweils anzuzeigende Frequenz ausgewählt werden.

Eine Besonderheit der Plotly Version ist die Anzeige der 3D-Koordinaten auf der Oberfläche der 3D-Visualisierung beim Drüberfahren mit der Maus. In der derzeitigen Implementierung werden dabei Azimuth und Elevations-Winkel sowie absoluter und relativer Gewinn für den gerade ausgewählten Punkt angezeigt.

Allerdings habe ich mit Plotly auch einige Workarounds gebraucht:

• Es gibt einen Bug im Koordinatendisplay

• Plotly unterstützt kein Menü (Legende) bei 3D Oberflächen, Ich musste eine zusätzliche (leere mit einem weissen Pixel) Grafik in die Anzeige aufnehmen um Menü (Legende) anzuzeigen. Das Menü wird verwendet um auf der rechten Seite die Anzeige für eine bestimmte Frequenz auszuwählen.

• In Plotly gibt es keine Möglichkeit, nur einen bestimmten Menüeintrag gleichzeitig anzuzeigen. Ich wollte dass sich die Menü-Einträge wie Radio-Knöpfe (Radio-Buttons) verhalten: Beim Klicken auf eine Frequenz sollte die Visualisierung von nur dieser Frequenz erfolgen. Für 3D Grafiken macht es nicht viel Sinn, mehrere 3D Visualisierungen in einer Anzeige zu haben. Dies wird mit ein paar Zeilen individuellem Javascript erreicht.

Das Antennendiagramm in obigem Beispiel ist aus einem Artikel von L.B. Cebik [2]. Beim Vergleich des Diagramms im Artikel mit obiger 3D-Ansicht fällt auf (auch ein Vergleich der Azimuth/Elevationsdiagramme in der Beschreibung von plot-antenna ist möglich) dass die Plotly 3D Ansicht leicht verzerrt ist (die Keule ist zu lang). Ich habe noch nicht rausgefunden ob das ein Problem von Plotly oder meiner Verwendung davon ist. Ich versuche das gleiche Bildseitenverhältnis für alle Richtungen einzustellen indem ich den Wertebereich (range) für xaxis, yaxis und zaxis einstelle aber es schaut nicht korrekt aus.

Beim Vergleich mit dem Azimuth Diagramm welches mit Plotly erzeugt wurde:

sehen die Größenverhältnisse richtig aus. Auch im 2D-Diagramm wird der Winkel (Azimuth in diesem Fall) beim Überfahren mit der Maus sichtbar. Auch mit Matplotlib ist dies möglich, jedoch rastet der Cursor nicht auf den jeweiligen Punkt auf der Anzeige ein. Damit kann mit Matplotlib nur geraten werden ob sich der Cursor an der korrekten Stelle befindet. Weiters kann wie bei der 3D-Grafik die Frequenz für die Anzeige rechts in der Legende ausgewählt werden. Diesmal ist die gleichzeitige Anzeige von mehreren Frequenzen möglich, was bei einer opaken 3D-Ansicht nicht sehr sinnvoll wäre.

[Änderung 2022-10-18: Ersetze epsilon durch delta in der Beschreibung von Beispiel 7 in pgapack]

Viele Optimierungsprobleme beinhalten Randbedingungen die von gültigen Lösungen erfüllt sein müssen. Ein Optimierungsproblem mit Randbedingungen wird typischerweise als nichtlineares Programmierungs-Problem formuliert [1].

In diesem Problem gibt es \(n\) Variablen (der Vektor \(\vec{x}\) hat die Länge \(n\)), \(J\) Ungleich-Bedingungen, \(K\) Gleichheits-Bedingungen und die Variable \(x_m\) muss im Bereich \(|x_m^l, x_m^u|\) sein (als Box-Bedingung bezeichnet). Die Funktionen \(f_i\) heissen Zielfunktionen. Probleme mit mehreren Zielfunktionen habe ich schon früher in diesem Blog [2] beschrieben. Im folgenden werde ich einige Begriffe ohne weitere Erklärung verwenden die in diesem früheren Blogbeitrag eingeführt wurden.

Die Zielfunktionen werden nicht notwendigerweise minimiert (wie in der Formel angegeben) sondern können auch maximiert werden wenn das Problem dies verlangt. Die Ungleich-Bedingungen werden auch oft mit einem \(\ge\) Zeichen formuliert, die Formal kann einfach umgestellt werden (z.B. durch Multiplikation mit -1) um ein \(\le\) Zeichen zu verwenden.

Nachdem es recht schwer ist, Gleichheits-Bedingungen zu erfüllen, besonders wenn diese in nichtlinearen Funktionen der Eingabevariablen auftreten, werden Gleichheits-Bedingungen oft in Ungleich-Bedingungen umgewandelt unter Verwendung einer δ‑Umgebung:

Wobei δ so gewählt wird dass die Lösung gut genug für das zu lösende Problem ist.

Eine sehr erfolgreiche Methode zur Lösung von Problemen mit Randbedingungen verwendet eine lexicographische Ordnung von Randbedingungen und Zielfunktion(en). Lösungskandidaten des Problems werden zuerst nach verletzten Randbedingungen sortiert (typischerweise der Summe der Verletzung von Randbedingungen) und dann nach dem Wert der Zielfunktion(en) [1]. Beim Vergleich von zwei Individuen während der Selektionsphase des Genetischen Algorithmus gibt es drei Fälle: Wenn beide Individuen die Randbedingungen verletzen gewinnt das Individuum mit der kleineren Verletzung der Bedingungen. Wenn ein Individuum keine Bedingung verletzt, das andere aber schon, gewinnt das Individuum ohne Verletzung von Randbedingungen. Im letzten Fall dass keines der Individuen die Bedingungen verletzt, findet ein normaler Vergleich der Zielfunktionen statt (was vom verwendeten Algorithmus abhängt und ob maximiert oder minimiert wird). Diese Methode, ursprünglich von Deb [1] vorgeschlagen ist in PGAPack und im Python Wrapper PGAPy implementiert.

Mit diesem Algorithmus zur Behandlung von Randbedingungen, werden zuerst Lösungskandidaten gefunden die keine Randbedingung verletzen bevor der Algorithmus die Zielfunktionen überhaupt "anschaut". Daher passiert es dann oft, dass die Suche in einer Region endet wo es keine guten Lösungen gibt (aber dafür keine Randbedingungen verletzt sind). Schwierige Probleme, bei welchen dies auftritt, sind oft Probleme mit Gleichheits-Bedingungen aber es gibt auch andere "schwierige" Randbedingungen. In einem früheren Blog Post [2] zur Antennen-Optimierung habe ich geschrieben: "dass der Optimierungs-Algorithmus Schwierigkeiten hat, überhaupt sinnvolle Lösungen für die Direktor-Variante zu finden. Nur bei einer handvoll Experimente war es überhaupt möglich, die obige Pareto-Front zu finden."

In diesem Experiment habe ich 50 Optimierungsläufe durchgeführt und nur 5 davon sind nicht in einem lokalen Optimum steckengeblieben. Etwas ähnliches passiert bei Problem 7 in Deb's Artikel [1] wo Gleichheits-Bedingungen verwendet werden. Ich habe dieses als Beispiel 7 in PGAPack implementiert. Es wird nur eine Lösung nahe dem (bekannten) Optimum gefunden wenn \(\delta \ge 10^{-2}\) für alle Gleichheits-Bedingungen ist (ich habe nicht mit verschiedenen Anfangswerten für den Zufallszahlengenerator experimentiert, es könnte sein dass man mit einem anderen Startwert bessere Lösungen findet). Im Artikel [1] verwendet Deb \(\delta = 10^{-3}\) aus dem selben Grund.

Eine Methode, um dieses Problem zu verbessern, war attraktiv, weil sie sowohl einfach zu verstehen als auch zu implementieren ist: Takahama und Sakai haben zuerst mit einer Methode experimentiert um unter gelockerten Randbedingungen in der Frühphase der Optimierung zu arbeiten, sie nannten dies einen Genetischen Algorithmus mit α‑Randbedingungen [3]. Die Methode wurde später vereinfacht und als Optimierung mit ε‑Randbedingungen bezeichnet. Sie kann für verschiedene Optimierungsalgorithmen verwendet werden, nicht nur für Genetische Algorithmen und Varianten [4]. Von speziellem Interesse in diesem Zusammenhang ist die Anwendung der Methode für Differential Evolution [5], [6], aber natürlich kann sie auch für andere Formen von Genetischen Algorithmen verwendet werden.

Das ε im Namen dieser Methode kann für das δ bei der Konversion von Gleichheits-Bedingungen in Ungleich-Bedingungen verwendet werden, ist aber nicht auf diesen Anwendungsfall eingeschränkt.

Während des Optimimierungslaufes wird in jeder Generation ein neuer Wert für ε berechnet. Der Vergleich von Individuen wie oben skizziert wird so modifiziert, dass ein Individuum so behandelt wird als verletze es keine Randbedingung wenn die Verletzung der Randbedingungen kleiner ist als ε. Wenn also beide Individuen die Randbedingungen um mehr als ε verletzen gewinnt das Individuum mit der kleineren Verletzung. Wenn ein Individuum die Bedingungen um weniger als ε verletzt, das andere aber mehr, gewinnt das erste. Und schließlich wenn die Verletzung der Randbedingungen bei beiden Individuen kleiner ist als ε findet der normale Zielfunktions-Vergleich statt.

Dieser letzte Fall ist der Schlüssel zum Erfolg des Algorithmus: Obwohl die Suche in eine Richtung zu weniger Verletzung der Randbedingungen fortschreitet, wird gleichzeitig eine gute Lösung bezogen auf die Zielfunktionenen gefunden.

Der Algorithmus startet mit der Initialisierung von \(\varepsilon_0\) mit der Summe der Verletzung der Randbedingungen des Individuums mit dem Index \(\theta\) der nach Verletzung der Randbedingungen sortierten initialen Population. Dabei ist \(\theta\) ein Parameter des Algorithmus zwischen 1 und der Populationsgröße, ein guter Wert ist etwa 20% der Populationsgröße, was auch der Standardwert in PGAPack ist. In jeder Generation \(t\) wird \(\varepsilon_t\) berechnet zu:

bis zur Generation \(T_c\). Nach dieser Generation wird ε auf 0 gesetzt. Der Exponent \(cp\) ist zwischen 2 und 10. Der Artikel von 2010 [6] empfiehlt zur Generation \(T_\lambda = 0.95 T_c\) den Wert \(cp = 0.3 cp + 0.7 cp_\min\) zu setzen, wobei \(cp_\min\) der fixe Wert 3 ist. Der Anfangswert von \(cp\) wird so gewählt dass zur Generation \(T_\lambda\) \(\varepsilon_\lambda=10^{-5}\) ist ausser \(cp\) wäre kleiner, dann wird es auf \(cp_\min\) gesetzt. PGAPack implementiert diese Empfehlung für \(cp\) als Standard-Einstellung, erlaubt aber das Setzen von \(cp\) zu Beginn und während der Laufzeit der Optimierung. Es ist also einfach möglich, andere Änderungen von \(cp\) zu implementieren – die Standard-Einstellung funktioniert jedoch recht gut.

Durch Optimierung mit ε Randbedingungen konnten in meinen Experimenten die Gleichheits-Bedingungen in Beispiel 7 von Deb [1] mit einer Genauigkeit von \(10^{-6}\) approximiert werden, siehe die Variable epsilon_generation im optimizer Beispiel.

Wird der antenna-optimizer mit ε‑generation 50 gestartet (das ist der \(T_c\) aus obigem Algorithmus) bleibt der Algorithmus nur in einem einzigen Fall im lokalen Optimum stecken, alle anderen Fälle finden gute Lösungen:

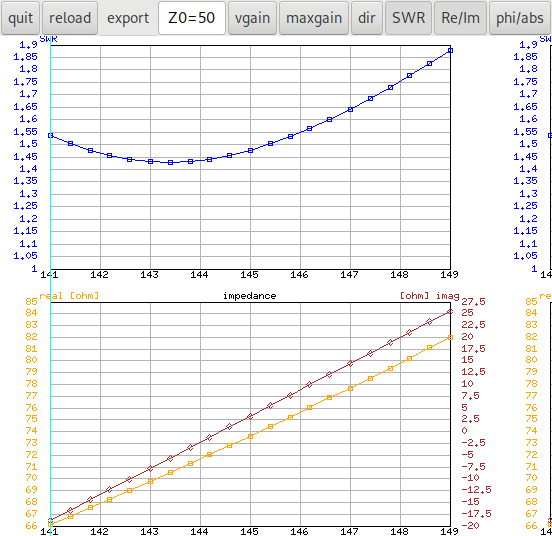
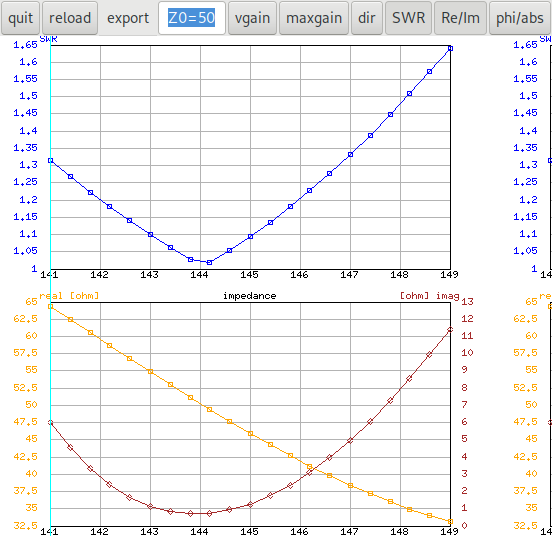
In dieser Grafik sind alle Lösungen von einem Optimierungslauf die von den Lösungen eines anderen Laufs dominiert werden in Schwarz eingezeichnet. Wir sehen dass die Daten von Lauf 16 keine nicht-dominierte Lösung beigetragen haben (auf der rechten Seite in der Legende fehlt die Nummer 16). In der Grafik kann man die dominierten Lösungen aus der Anzeige nehmen indem man auf den schwarzen Kreis in der Legende klickt.

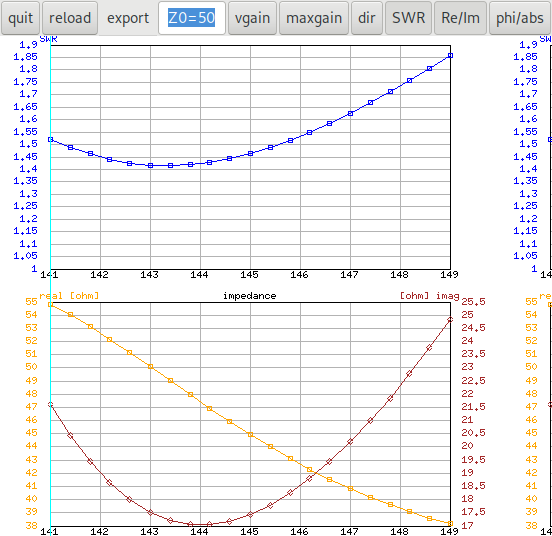
Wenn der Parameter ε‑generation für den Lauf der im lokalen Optimum geendet hat auf 60 erhöht wird, findet auch der Lauf mit Zufallszahlen-Startwert 16 eine Lösung:

Es ist auch sichtbar dass die Lösungen für alle Experimente ziemlich gut (weil nahe an der Pareto-Front) sind. Der schwarze "Schatten" der dominierten Lösungen ist ziemlich nahe an der wirklichen Pareto-Front und ist gut genug um mit einem einzigen Optimierungslauf ausreichend gute Lösungen zu finden.

Vor kurzem waren in der deutschen Zeitschrift "Funkamateur" zwei Artikel wo der Autor behauptet hat, es sei möglich, ein besseres Stehwellenverhältnis (SWV) mit Hilfe eines 50Ω Kabels zu erreichen.

Der erste Artikel beschrieb eine Duoband-Antenne für die 70cm und 2m Amateurfunkbänder [1]. Der Artikel erwähnte nebenbei dass das SWV durch eine spezifische Länge von 50Ω Kabel verbessert werden könne und enthielt einen Link zu einer Software des selben Autors um diese Länge zu berechnen (es wurde behauptet dass verschiedene Längen von Kabel für den zu erreichenden Zweck möglich seien). Die Behauptung war, es fände eine Leitungstransformation durch das 50Ω Kabel statt.

Im zweiten Artikel – ausgelöst von mehreren Lesern die Leserbriefe geschrieben hatten – lieferte der Autor Messergebnisse die klar zeigten dass, in der Tat, das SWV durch eine bestimmte Kabellänge verbessert wurde [2].

Nun sagt die Leitungstheorie dass eine Impedanztransformation mit Änderung des Stehwellenverhältnisses nur mit einer Leitung einer anderen Impedanz als der Systemimpedanz erreicht werden kann, siehe auch meinen kürzlich erschienenen Artikel zu diesem Thema. Es muss also einen anderen Grund geben, warum sich die Impedanz ändert – wie klar von den Messungen des Autors gezeigt wurde. Der Autor meint in seinem Artikel dass es wohl eine Diskrepanz zwischen Theorie und Praxis gäbe – ich zeige im folgenden dass es eine ganz gute Erklärung für die Beobachtungen gibt ohne die existierende elektromagnetische Theorie über Bord zu werfen.

Der Hinweis hier ist, dass der Autor keinen Balun oder einen anderen Mechanismus zur Unterdrückung von Mantelwellen auf der Zuleitung verwendet hat. Also habe ich mir den Spaß gemacht, die Verhältnisse mit dem Antennen-Simulationsprogramm NEC2 zu simulieren. Die Resultate sollten mit einem anderen Modellierungsprogramm reproduzierbar sein, zumindest wenn dieses einen NEC Kern (z.B. EZNEC) enthält der auch ein Bodenmodell enthält und nicht nur im Freiraum simulieren kann. Ich habe die (einfache Zwei-Elemente) Antenne aus dem Original-Artikel modelliert.

Die folgende Grafik zeigt das Stehwellenverhältnis (SWV) und den Real- und Imaginäranteil der Impedanz direkt an der Antenne. Das erste NEC input file kann verwendet werden um die Resultate zu reproduzieren. Ich habe das Sommerfeld/Norton Bodenmodell mit einer mittleren Bodenqualität verwendet. Die Antenne ist 15m über dem Boden in diesem Modell weil sie zur Befestigung auf einem Balkon vorgesehen ist.

Das nächste Bild zeigt die selbe Antenne mit einem Stück Speiseleitung (die Länge ist die von der der Autor behauptet sie würde das SWV verbessern). Die Speiseleitung ist nicht als Draht modelliert, sondern als Übertragungsleitung (für die bietet NEC eine eigene Abstraktion). Wieder zeigen wir Real- und Imaginärteil der Impedanz. Die elektrische Länge (NEC verwendet bei Übertragungsleitungen die elektrische Länge ohne Verkürzungsfaktor) ist etwa 1.81m berechnet mit der Formel aus [1] mit einem Verkürzungsfaktor von 1. Es ist klar ersichtlich, dass sich zwar die Impedanz ändert aber das SWV gleich bleibt. Das korrespondierende zweite NEC input file kann auch hier verwendet werden um die Resultate zu reproduzieren.

Um nun die Verhältnisse am Speisepunkt zu simulieren wenn es keinen Balun gibt habe ich einen Draht zwischen der Antenne und dem Speisepunkt am Ende des Kabels im dritten NEC input file modelliert. Das folgende Bild zeigt das Modell, wir haben einen zusätzlichen Draht der die Aussenseite der Coax-Speiseleitung darstellt. Dieser Draht ist verbunden mit der Antenne auf der einen Seite und dem Ende des Coaxkabels auf der anderen Seite. Die Länge des Kabels ist die physikalische Länge. Ausser einer geringfügigen Erhöhung der elektrischen Länge wegen der Isolation (nicht mit dem üblichen Coax Verkürzungsfaktor, wir simulieren ja nur das äussere Drahtgeflecht!) muss der Draht im Modell die echte physische Länge des Coax wie mit der Formel aus dem ersten Artikel berechnet [1] verwenden. Wir verwenden 1.484m aus [1], Tabelle 3 für ein Aircell5 mit dem Faktor n=1 aus der Tabelle im Artikel. Wir sehen dass sich in der Tat, wie im zweiten Artikel [2] beobachtet, das Stehwellenverhältnis SWV verkleinert hat. Der Grund ist dass, wegen des fehlenden Balun, sich die Antenne geändert hat: Der Aussenmantel der Coax-Speiseleitung ist Teil der Antenne.

Wenn man sich die Antenne mit dem Linux-Programm xnec2c ansieht, bemerkt man die Ströme auf der Aussenseite der Speiseleitung. Wir können klar sehen, dass da ein Strom auf der Speiseleitung fließt (die Speiseleitung in dem Bild ist der lange Teil rechts, parallel dazu liegt die modellierte Übertragungsleitung zur Speisung).

Also ist die elektromagnetische Theorie gerettet, es gibt eine physikalische Erklärung des Phänomens. Trotzdem wäre es noch interessant die verschiedenen Einflüsse von Höhe über Grund oder unterschiedliche Bodencharacteristika zu modellieren – um herauszufinden wie reproduzierbar die Ergebnisse mit unterschiedlichen Parametern sind , weil der Autor ja behauptet das beobachtete Verhalten sei "seit Jahren bekannt" ([2] S. 35).