Q-Faktor eines Coax Resonators

Ralf Schlatterbeck 2021-10-11 10:30

Auch verfügbar in:

[Edit 2021-10-25 Tippfehler gefixt, Danke Peter!]

Als ich vor kurzem Übertragungsleitungen für mein antenna-optimizer Projekt studiert habe, bin ich über eine Formel für den Q-Faktor eines Coax-Resonators von Frank Witt [1] gestolpert:

\begin{equation*} \frac{2.774 F_0}{A \cdot \mathbb{VF}} \end{equation*}

In dieser Formel ist \(F_0\) die Frequenz des Resonators in MHz, \(A\) is der Verlust in dB pro 100 ft, und VF ist der velocity factor (oder auf Deutsch "Verkürzungsfaktor") des Kabels. Die Formel war für einen \(\frac{\lambda}{4}\) Resonator angegeben. Ich habe mich über die Formel gewundert, weil ich dachte dass ein logarithmischer Wert für den Verlust eine Exponentiation bei der Berechnung des Q-Faktors erfordern sollte.

Wenn wir bei Wikipedia die Definition der Güte eines Schwingkreises nachschlagen bekommen wir:

\begin{equation*} 2 \pi \frac{E_s}{E_d} \end{equation*}

Wobei \(E_s\) die gespeicherte Energie ist und \(E_d\) die während der Schwingung als Wärme verbrauchte Energie.

Wir wissen, dass der Verlustfaktor eines Kabels in dB Leistungsverluste definiert. Wenn der Verlust in dB pro 100m (wir verwenden natürlich metrische Einheiten) \(a\) ist, haben wir für den Verlust in dB:

\begin{equation*} \frac{a \cdot l}{100} \end{equation*}

Wobei \(l\) die Länge in Meter ist. Für einen \(\frac{\lambda}{4}\) Resonator bekommen wir:

\begin{equation*} \frac{a \cdot \mathbb{VF}\lambda}{4\cdot 100} \end{equation*}

Um die Verlustleistung als Faktor zu bekommen (statt in dB) bekommen wir:

\begin{equation*} 1 - 10^{-\frac{a \cdot \mathbb{VF}\lambda} {4 \cdot 100 \cdot 10}} \end{equation*}

Wir setzen

\begin{equation*} \lambda = \frac{c}{f_0} \end{equation*}

in die Formel ein, wobei \(c\) die Lichtgeschwindigkeit ist und \(f_0\) die Resonanzfrequenz in Hz:

\begin{equation*} 1 - 10^{-\frac{a \cdot c\cdot\mathbb{VF}} {4 \cdot 100\cdot 10\cdot f_0}} \end{equation*}

Zurück zur Wikipedia-Formel die ja Energien benötigt müssten wir hier integrieren – aber weil beim Integrieren eines Verhältnisses wieder das selbe Verhältnis rauskommt machen wir so eine Art vereinfachende Integration wo wir uns nur überlegen müssen wie lang die von der Energie zurückgelegte Distanz ist. Die Wikipedia-Definition behandelt eine volle Periode, also \(\lambda\), nicht \(\frac{\lambda}{4}\). Und der Q-Faktor ist das Verhältnis von gespeicherter zu verlorener Energie. Wir haben also:

\begin{equation*} Q = \frac{2\pi}{1 - 10^{-\frac{a \cdot c\cdot\mathbb{VF}}{1000\cdot f_0}}} \end{equation*}

Wie wir sehen ist das \(Q\) des Resonators unabhängig vom Resonator-Typ, sei es ein \(\frac{\lambda}{4}\) oder \(\frac{\lambda}{2}\) Resonator.

Wenn wir Q-Faktoren für einige Kurzwellen-Frequenzen (in der Grafik sind die Frequenzen in MHz) gegen Verluste in dB auftragen, sehen wir dass obige Formel recht nahe bei der Näherungsformel von Witt [1] ist.

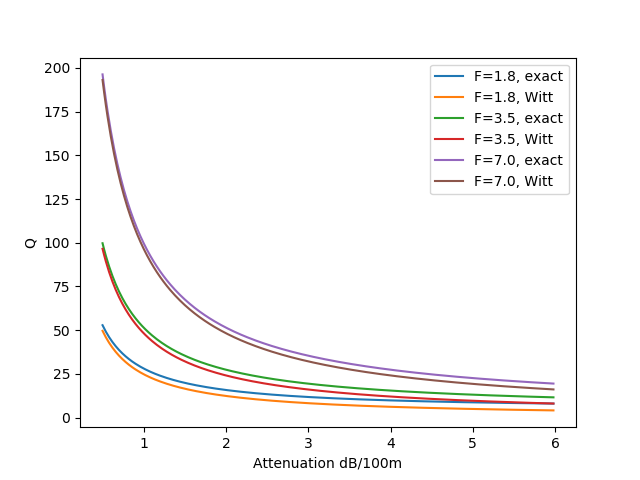
Plotten wir den Q-Faktor gegen die Frequenz (auch im Kurzwellen-Bereich) für typische Kabel, sehen wir auch dass der Fehler nicht sehr hoch ist, jedenfalls bei höheren Frequenzen.

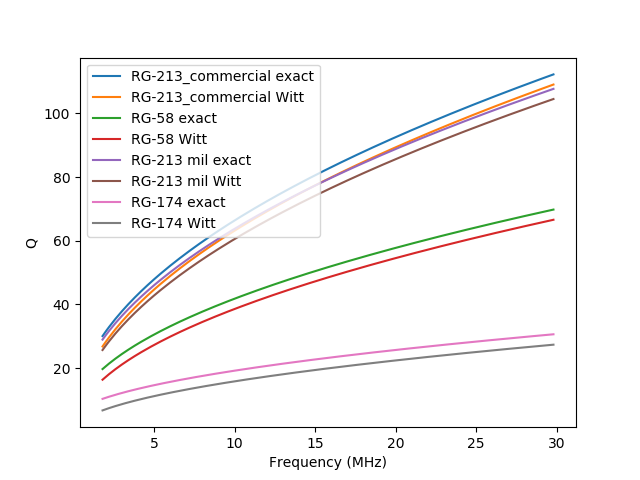
Den relativen Fehler können wir auch darstellen, wieder für typische Kabel über den gesamten Kurzwellenbereich. Wir sehen, dass der Fehler recht hoch ist für niedrige Frequenzen und verlustreiche Kabel wie RG174.

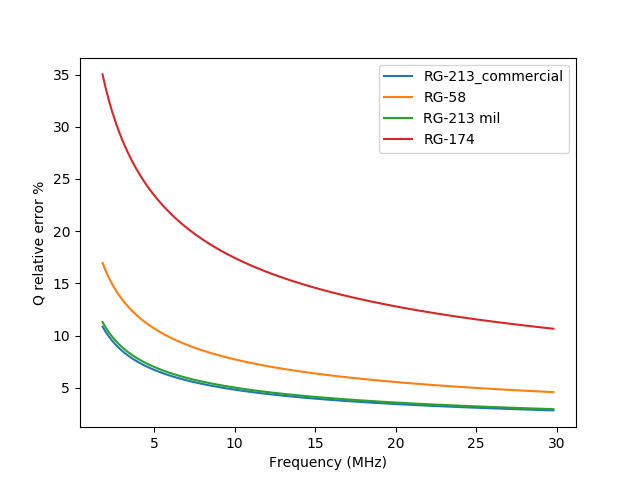
Wir sehen also dass Witts Formel vermutlich eine Approximation ist, die recht gut für hohe Frequenzen und niedrige Verluste funktioniert. Die Frage ist aber offen: Woher kommt die Formel und woher kommt die magische Konstante die vermutlich alle physischen Konstanten in der Formel zusammenfasst?

Beim Studium von Übertragungsleitungen bin ich auch über ein älteres Buch gestolpert, das mal ein Universitäts-Lehrbuch war [2]. Auf S. 222 leitet Chipman eine Näherungsformel für \(Q\) her, die als vereinfachende Annahme ein niedriges \(\alpha\) (den Dämpfungskoeffizienten in Neper) voraussetzt. Chipman's Näherungsformel ist:

\begin{equation*} Q \approx\frac{\beta_r}{2\alpha_r} \end{equation*}

Hier ist \(\alpha\) der Dämpfungskoeffizient in Neper/m und \(\beta\) ist der Phasenfaktor in Radians pro Meter. Das Subscript \(r\) steht für Resonanz. Wir schreiben:

\begin{equation*} \lambda=\frac{c\mathbb{VF}}{f_0} \end{equation*}

und

\begin{equation*} \beta_r=\frac{2\pi}{\lambda} \end{equation*}

und Witts Verlust \(A\) pro 100 ft können wir auch schreiben (wir konvertieren Neper zu dB) als:

\begin{equation*} A=\frac{20\cdot 100\alpha_r}{3.2808\cdot log_e 10} \end{equation*}

Wobei die Konstante 3.2808 der Konversionsfaktor m/ft ist. Lösen wir für \(\alpha_r\) und ersetzen \(\lambda\) und \(\alpha_r\) in Chipman's Formel bekommen wir:

\begin{equation*} Q \approx\frac{2\cdot 2000\pi f_0} {2 c \mathbb{VF}\cdot A \cdot 3.2808\cdot log_e 10} \approx\frac{2.774 F_0}{A \mathbb{VF}} \end{equation*}

Wobei das \(F_0\) die Frequenz \(f_0\) in MHz ist.

Wir sehen dass die Annahme von niedrigem \(\alpha\) in Chipman's (und Witt's) Formel für höhere Frequenzen und niedrige Verluste zutrifft: \(\alpha\) in Neper pro Meter ist ein konstanter Faktor wenn wir es in dB (pro 100m oder pro 100 ft) umrechnen. Dass die Näherung mit hohen Frequenzen besser wird, liegt daran, dass Kabelverluste typischerweise mit der Wurzel aus \(\lambda\) steigen, während \(\lambda\) invers proportional mit der Frequenz sinkt. Also hat z.B. ein \(\frac{\lambda}{4}\) Resonator höhere Verluste bei niedrigen Frequenzen.

Runtux Blog credits